Луна в роли ускорителя

Ограниченная задача трех тел - Земля - Луна - космический аппарат является наглядным источником сюрпризов для изучающих космическую баллистику.

Ранее мы уже неоднократно касались вопроса о том, что после того, как космический аппарат "побывает" в сфере действия Луны, его дальнейшее движение может быть самым неожиданным. Первоначальная траектория движения начисто ломается, скорость полета, пространственное положение орбиты и форма ее после выхода из сферы действия уже ничего не имеют общего с первоначальными характеристиками движения. Такого рода "ломка", конечно, не является случайной, она 'подчинена строгим законам небесной механики и зависит от условий входа в сферу действия Луны. Чем меньше скорость входа в сферу действия и чем ближе траектория проходит относительно Луны, тем сильнее проявляется эффект ее влияния. Однако, кроме очевидного эффекта - искривления траекторий, Луна по отношению к космическому аппарату может выступать в качественно новой роли, становясь своеобразным генератором или потребителем механической энергии. Это проявляется в том, что космический аппарат на выходе из сферы действия Луны, за исключением отдельных частных случаев, по отношению к Земле будет иметь другой запас механической энергии по сравнению с той, с которой он входил в сферу действия. Иначе говоря, суммы кинетической и потенциальной энергии его на входе в сферу действия Луны и на выходе из нее не будут равны между собой. Откуда же берется или куда отдается эта энергия? Несколько раньше мы уже поясняли это обстоятельство: изменение механической энергии движения космического аппарата происходит за счет соответствующего увеличения или уменьшения энергии Луны. Когда энергия аппарата возрастает, то на ту же самую величину уменьшается энергия движения Луны, в результате чего Луна как -бы замедляет свой бег относительно Земли.

Теперь мы можем провести качественный анализ вопроса - при каких направлениях входа космического аппарата в сферу действия Луны возрастание его геоцентрической энергии будет наибольшим?

Пусть траектория отлета от Земли выбрана так, что космический аппарат после пересечения сферы действия Луны двигается вдоль прямой, соединяющей центры Земли и Луны (рис. 91). Войдя в сферу действия в точке А со скоростью V (относительно Луны), он выйдет в диаметрально противоположной точке А′ с точно такой же скоростью (при этом предполагаем, что он не столкнулся с Луной). Поскольку скорости входа и выхода одинаковы, го кинетическая энергия космического аппарата относительно Земли останется одной и той же. В то же время из-за увеличения расстояния до Земли (точка А лежит от Земли на 132 тыс. км дальше, чем точка А) потенциальная энергия возрастет.

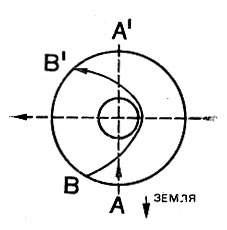
Рис. 91. Полет внутри сферы действия Луны

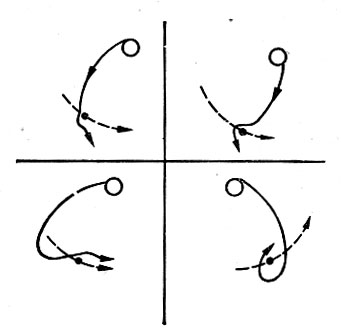
Рис. 92. Классы траекторий максимального разгона с помощью Луны

Рассмотрим, далее, второй случай, когда вход в сферу действия Луны осуществлен в точке В так, что внутри нее космический аппарат движется по сильно изогнутой гиперболической траектории и на выходе из сферы действия скорость его примерно совпадает с направлением движения Луны. Помимо очевидного увеличения потенциальной энергии у космического аппарата здесь произойдет увеличение и кинетической энергии, поскольку к собственной скорости движения относительно Луны на выходе из сферы действия Луны прибавится еще скорость Луны.

Таким образом, чтобы добиться наибольшего повышения энергии космического аппарата за счет энергии Луны, необходимо отлетные от Земли траектории выбирать так, чтобы движение внутри сферы действия Луны происходило по гиперболе типа ВВ′. Типичный вид таких траекторий показан на рис. 92. Наибольшему разгону соответствуют траектории, проходящие близко от поверхности Луны. При сближении с Луной на восходящей ветви космический аппарат должен обходить ее против часовой стрелки, а при сближении на нисходящей ветви - по часовой. Наиболее сильные разгонные траектории будут получаться в тех случаях, когда после выхода из сферы действия Луны скорость полета аппарата станет возможно ближе к направлению скорости Луны. Тогда к скорости выхода из сферы действия Луны добавится скорость движения Луны, относительно Земли. Получающаяся после разгона скорость относительно Земли всегда является гиперболической, т. е. после встречи с Луной космический аппарат навсегда уходит от Земли. И этот эффект всегда будет иметь место, независимо от начальной скорости полета с Земли, лишь бы соблюдалось указанное условие полета к Луне и облета ее. Однако величина скорости, на которую производится разгон, зависит и от начальной скорости отлета от Земли. Она достигает своего максимального значения (порядка 1,5 км/сек) при начальных, скоростях отлета, близких к минимальным. С ростом начальной скорости величина доразгона убывает, поскольку Луна оказывается уже не в состоянии должным образом повернуть подлетную траекторию к направлению своего движения.

Космический аппарат может стартовать с Земли в любой день каждого месяца, причем траектории полета его к Луне, обеспечивающие наибольший доразгон, будут примерно одними и теми же. Поэтому скорость отлета от Луны благодаря месячному вращению ее можно получить в любом направлении, лежащем в плоскости орбиты Луны. Поскольку эта плоскость составляет небольшие углы с плоскостями орбит планет, то ускоряющее влияние Луны может быть использовано для разгона космического аппарата с целью осуществления полетов к планетам Солнечной системы.

Необходимо, однако, оговориться, что реализация разгонных траекторий для дальних полетов является очень сложным делом. Как мы уже говорили, наиболее сильные разгонные решения получаются при близком облете Луны. Повышение траектории над Луной уменьшает выигрыш в скорости. Значит, чтобы добиться максимального разгона, необходимо очень точно вывести ракету на траекторию полета к Луне или, если это технически нереально, осуществлять коррекцию ее перед сближением с Луной.

В заключение отметим, что решение задачи о любом разгоне вследствие обратимости движения всегда дает также решение задачи о таком же торможении с помощью Луны при движении по траектории, зеркально симметричной разгонной. При этом наиболее выгодной для торможения оказывается траектория, получающаяся из наиболее выгодной разгонной. Траектории максимального торможения могут быть использованы, например, при возвращении .космического аппарата из межпланетного полета.