Глава 2. Оценка возможностей телескопа

Предположим, что у Вас есть телескоп, снабженный экраном или фотокамерой, а возможно и спектрографом. Вас, конечно, интересует, какие полезные для развития астрономии задачи Вы можете решать.

Но прежде чем приступить к выбору задачи, Вы должны уяснить себе возможности Вашей аппаратуры и места наблюдения и постараться выразить их количественно. Под аппаратурой я понимаю не только телескоп с приемными устройствами, но и приборы для обработки наблюдений (от карандаша и линейки до микрофотометра).

Итак, начнем с телескопа. Об основных характеристиках его мы говорили в начале предыдущей главы. Теперь попробуйте определить характеристики Вашего телескопа, перечисленные в табл. 3. Я заполню эту таблицу для телескопа-рефрактора, характеристики которого мы использовали в примерах главы 1.

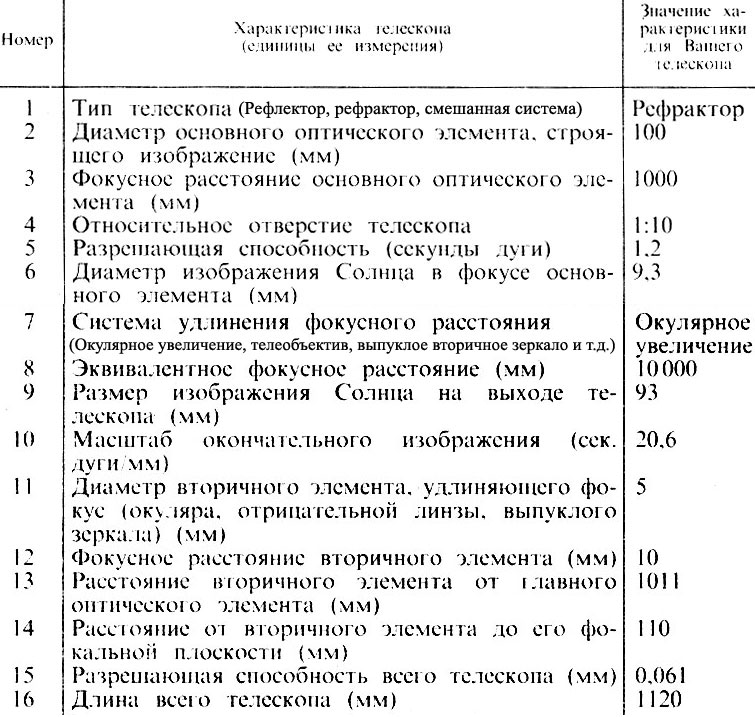
Таблица 3

Аналогичную таблицу можно составить для спектрографа.

Кроме характеристик телескопа надо знать, какими фотоматериалами Вы располагаете, каковы их характеристики (общая чувствительность, спектральная чувствительность и размеры зерна) Немаловажное значение имеют и атмосферные условия в месте наблюдения, так называемый астроклимат. Любителю астрономии, конечно, трудно провести исследование астроклимата по полной программе, как это делают астрономы при выборе места для обсерватории. Но две-три характеристики можно получить. Первая характеристика это дрожание изображения. Нужно положить себе за правило перед началом каждого наблюдения приложить кусок миллиметровой бумаги к краю изображения Солнца и определить, в каких пределах колеблется край, переведя лгу величину из миллиметров в секунды дуги в соответствии с п. 10 таблицы 3. Регулярно записывая величину дрожания, вы сможете определить среднее дрожание и изменение его со временем. Вторая характеристика качество изображения. Это довольно субъективная характеристика. Обычно оценивают качество изображения по пятибалльной шкале, как отметки в школе. 5 наилучшие изображения, когда четко видны все тонкие детали, размер которых почти совпадает с разрешением телескопа. Это могут быть отдельные гранулы или скопления гранул, тонкая структура полутени пятна, резкость края диска. 1 - наихудшие изображения, когда все детали размыты. Вся шкала оценок от 5 до 1 вырабатывается каждым наблюдателем постепенно, по мере накопления опыта. Третья характеристика- состояние неба: наличие облаков, дымки, прозрачность атмосферы. Эти данные тоже следует записывать регулярно во время наблюдений. Со временем вы сможете четко, сказать, что, например, "наилучшие наблюдения получаются в утренние часы в первой половине августа. В это время можно увидеть детали на Солнце размером 1,5-2 секунды дуги". Затем встает вопрос, с какой точностью вы сможете измерить положение деталей на Солнце и их размер. Например, если телескоп может разрешить детали изображения, отстоящие друг от друга на 0,06 мм, а измерять расстояния вы можете линейкой с миллиметровыми делениями, то ясно, что об определении размеров тонкоструктурных образований с такой "измерительной техникой" говорить не приходится. В то же время при масштабе изображения Солнца 20 секунд дуги на мм с помощью линейки вы можете определить расстояние пятна от центра диска с точностью 0,3-0,5 мм, т. е. 6-10", что для многих задач вполне пригодная точность.

В любом случае, какими бы измерительными средствами вы ни располагали, надо заранее знать точность ваших измерений. Обратимся к простейшему примеру. Ваш телескоп построил изображение Солнца на экране. Вы хотите измерить диаметр большого солнечного пятна. Прикладывая линейку с миллиметровыми делениями или кусок миллиметровой бумаги к экрану, вы определили, что диаметр пятна 7 мм. Но так как изображения Солнца и пятна дрожат, то измерив диаметр пятна во второй раз, вы получите какое-то другое значение. Для определения диаметра вам следует измерить его не менее трех раз, а лучше и пять, записывая каждый раз получившееся значение. Каждое такое отдельное измерение обозначим через x_i, где i - порядковый номер вашего измерения (i=1, ..., n; если вы измеряли 5 раз, то n = 5). Из этих индивидуальных измерений находим среднее значение 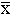по формуле

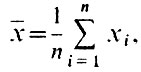
т. е. 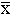равно сумме всех измерений, деленной на число измерений. Но полученное значение еще ничего не говорит о точности ваших измерений. Теперь надо определить среднеквадратическую погрешность определения этого среднего значения. Она обычно обозначается греческой буквой σ и определяется по формуле

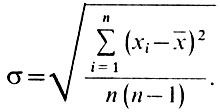
Зная 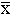и σ, запишем результат нашего измерения в виде 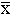± σ. Так, в случае измерения диаметра пятна предположим, что измерив его 5 раз, вы получили числа в миллиметрах: 7; 6,5; 6,7; 7,2; 7,4. Тогда

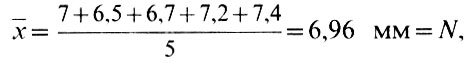
a

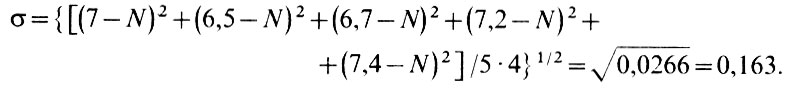
Теперь мы можем написать, что диаметр нашего пятна D_п1 =6,96±0,16 мм. Если через какое-то время в тот же или следующий день мы получим для того же пятна D_п2 = 7,10 мм, то не сможем уверенно говорить о росте пятна, так как разница D_п1 - D_п2 =0,14 мм меньше, чем погрешность измерения σ. В этом случае говорят, что D_п2 и D_п1 значимо не отличаются. Принято, что о значимом отличии величин можно говорить, если их разность превышает Зσ.

При фотографических наблюдениях мы сталкиваемся с несколько иной ситуацией. Предположим, вы не просто построили изображение Солнца на экране, но и сфотографировали на пластинку область Солнца с большим пятном. Если теперь вы измерите 5 раз один и тот же негатив, то получите ст меньше, чем в случае визуальных измерений. Это естественно. Ведь негатив не дрожит, и в ваши измерения входит только ваша личная ошибка, т. е. ошибка, с которой вы измеряете постоянную величину. Эта ошибка называется ошибкой наведения. Но если вы получите подряд 5 негативов и получите для каждого из них средние значения диаметра пятна и ошибки наведения, то увидите, что эти средние значения отличаются между собой больше, чем полученные ошибки наведения. Это тоже естественно, так как каждый негатив получен при разном дрожании, а следовательно, пятно по-разному "размазано" на негативе и имеет разный диаметр.

Сказанное выше приводит к тому, что получение диаметра пятна по фотографическим наблюдениям содержит следующие операции:

1. Получение нескольких негативов за короткий интервал времени.

2. Измерение каждого негатива несколько раз и получение 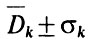наведения, где к - номер негатива, k = 1, ..., n, n - число негативов.

3. Повторение операции нахождения среднего и ошибки по значениям 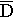_k

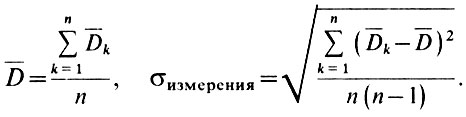
Теперь мы получили среднее значение диаметра пятна и погрешность его определения. Работа получилась более продолжительной, но точность полученного результата выше. Следует заметить, что если вы получили ошибку наведения больше, чем погрешность измерения, то вы плохо измеряете, надо принимать какие-то меры к повышению точности измерений. Телескоп позволяет измерять точнее.

Какие же меры можно принять? Самое простое - измерять расстояния не по негативу, а по его увеличенному изображению с помощью фотоувеличителя или проектора для диапозитивов.

Мы рассмотрели самый простой пример.

В своей работе вы встретитесь с различными измерениями положений, размеров, разностей двух величин и т. д. Прежде чем взяться за измерения, подумайте, какие величины и их изменения вы хотите измерить, как это согласуется с разрешением вашего телескопа, качеством изображения и точностью измерений. Получив результат, обязательно оцените ошибки измерений и наведений. Если результат ваших измерений - график, на котором показано изменение какой-то величины со временем или с расстоянием, то у каждой точки, представляющей одно измерение, должна стоять черточка, показывающая погрешность измерения, отложенную вверх и вниз. На рис. 19 показано изменение диаметра пятна D_п день ото дня. Каждая точка с черточкой представляет значение D_п±σ.

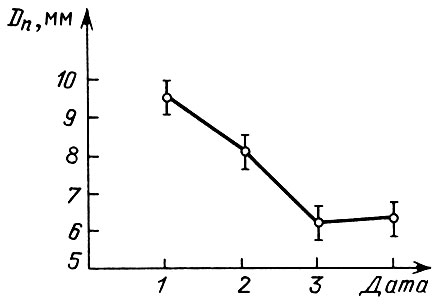
Рис. 19. Пример представления результатов измерений диаметра пятна в течение четырех дней