Масштабы мироздания

Угловые измерения сами по себе еще не дают представления о размерах небесных тел. На небе Солнце и Луна выглядят одинаковыми кружочками поперечником около 0,5°. Какое из светил больше или дальше, сразу не скажешь. Кроме угловых нужно знать еще линейные размеры, или расстояние до светил. Астрометрия, оставляя в стороне вопрос о физической природе небесных тел, позволяет узнать их удаленность и настоящие размеры. Иначе говоря, благодаря астрометрии мы можем наглядно представить себе масштабы Вселенной. Знаменитый древнегреческий астроном Эратосфен был, по-видимому, первым, кто (около 250 г. до н. э.) измерил размеры земного шара.

Принцип определения размеров Земли достаточно прост (рис. 22). Допустим (в первом приближении), что Земля - шар. Выберем два пункта А и С, расположенных на одном меридиане на расстоянии d друг от друга (AC = d). Пусть из этих пунктов одновременно в момент кульминации наблюдается Солнце, причем в пункте С оно находится в зените, а в пункте А - на зенитном расстоянии 7°. Выразим этот угол в радианах и обозначим его буквой α. Составляя очевидную пропорцию

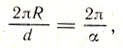
находим из нее радиус земного шара (в километрах):

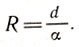
Эратосфен нашел, что длина земного экватора равна 250 000 греческих стадий, что близко к 45 000 км. Точность для первого измерения очень неплохая.

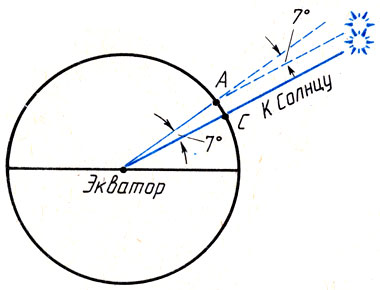
Рис. 22. Способ Эратосфена

Позже подобные градусные измерения, как их называют, повторялись много раз со все возрастающей точностью. Иногда на них тратились годы и десятилетия. Так, скажем, в 1735 г. Парижская Академия наук организовала две экспедиции - одну в Перу, в район экватора, другую в Лапландию, к полярному кругу. Целью экспедиций было измерение длины дуги одного градуса меридиана. Перуанская экспедиция работала 7 лет, Лапландская - год. По данным первой из них длина одного градуса меридиана получилась,. равной 110,6 км, по результатам второй 111,9 км.

Обратите внимание на заметную разницу в результатах. Вызвана она тем, что Земля сплющена у полюсов и приближенно имеет форму сфероида (рис. 23)^*. Следовательно, кривизна меридиана у экватора меньше, чем у полюсов. Отсюда проистекает и различие в линейной длине одного градуса меридиана. Таким образом, астро-метрические измерения позволяют узнать не только размеры Земли, но и ее форму.

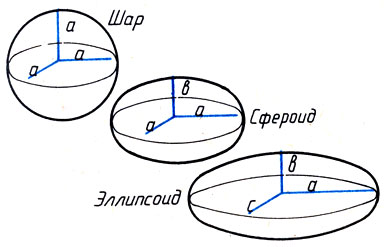
Рис. 23. Модели Земли

^* (У сфероида экватор - это окружность, а меридианы - эллипсы. )

Огромная работа по измерению дуги меридиана между Дунаем и Ледовитым океаном была выполнена знаменитым пулковским астрономом Василием Яковлевичем Струве (1793-1864). На нее ушло почти 40 лет, и результаты измерений были опубликованы лишь в 1861 г. Работа В. Я. Струве отличалась такой тщательностью выполнения и такой точностью, что измеренная дуга длиной более 2800 км получила в дальнейшем наименование дуги Струве.

Другой способ определения размеров Земли предложил выдающийся хорезмийский ученый-энциклопедист Бируни (973-1048). Он основан на явлении понижения видимого горизонта при подъеме наблюдателя на гору. Идея способа проста.

Пусть OB = R - радиус земного шара (рис. 24), а наблюдатель находится на высоте H = AD. Угол понижения горизонта ЕАВ = α равен углу при центре Земли BOD. Отсюда 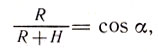откуда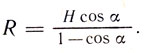

В сочинении под названием "Канон Масуда" Бируни приводит результаты измерения средней длины дуги, равной одному градусу меридиана. По его способу она составляла 111,6 км, что лишь на 0,5 км больше современного ее значения.

Еще Аристарх Самосский (310-250 гг. до н. э.) в сочинении "О величинах и расстояниях Солнца и Луны" предложил метод определения относительной удаленности этих небесных тел по лунным фазам. Так как моменты этих фаз (первой и последней четверти) определить очень трудно, результаты вычислений Аристарха получились грубо ошибочными. Греческий ученый пришел к выводу, что Солнце находится от нас всего в 20 раз дальше Луны (на самом деле в 400 раз). Позже расстояния до небесных тел стали определять таким же методом, как и расстояния до недоступных земных предметов.

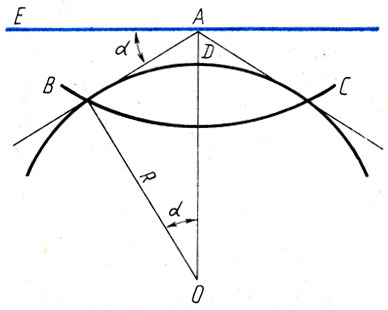
Рис. 24. Дальность видимого горизонта

Допустим, что надо определить расстояние до предмета на другом берегу реки, не переплывая реку (рис. 25). Для этой цели выбираем отрезок АВ, называемый базисом, и измеряем его длину. Затем из концов базиса А и В с помощью какого-нибудь угломерного инструмента измеряем углы между базисом и лучами, идущими из точек А и В на предмет С, расположенный на противоположном берегу. В треугольнике ABC теперь известны стороны АВ и два угла при этой стороне. В таком треугольнике можно определить длину его сторон, или, иначе говоря, расстояние до недоступного предмета С.

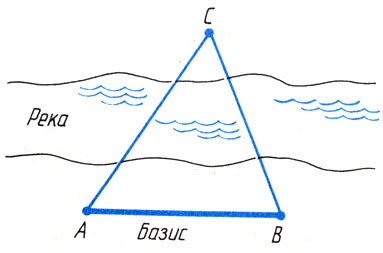
Рис. 25. Определение расстояния до недоступного предмета

Подобный принцип применяется и в астрономии.

Если перемещаться вдоль базиса АВ, то будет казаться, что предмет С смещается на фоне более далеких предметов. Такое кажущееся смещение предмета, вызванное перемещением наблюдателя, называется параллактическим, а угол, под которым с недоступного предмета виден базис,- параллаксом. Очевидно, что чем дальше предмет (при одном и том же базисе), тем меньше его параллакс.

Таким образом, для определения расстояния до недоступного предмета надо возможно точнее измерить его параллактическое смещение при наблюдении с концов известного базиса.

Даже самые близкие к нам небесные тела находятся на чрезвычайно больших расстояниях от Земли. Поэтому для измерения их параллактического смещения необходим очень большой базис.

При перемещении наблюдателя по земной поверхности на расстояния в тысячи километров происходит заметное параллактическое смещение Солнца, планет и других тел Солнечной системы.

Пусть какое-то тело Солнечной системы наблюдается с Земли из пунктов А и В, расположенных на одном меридиане. Измерив зенитные расстояния z₁ и z₂, зная разность широт пунктов А и В, можно вычислить все углы в четырехугольнике OBSA (рис. 26). Кроме того, учитывая, что в этом четырехугольнике две стороны ОА и ОВ равны радиусу Земли, можно определить все другие его стороны и искомую диагональ OS.

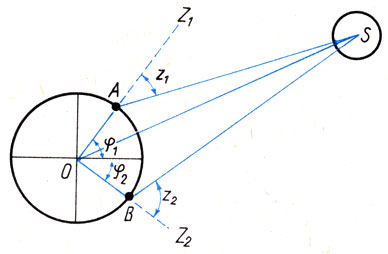
Рис. 26. Определение расстояния до близких небесных тел: А и В - пункты наблюдения, О - центр Земли, S - небесное тело, φ₁ и φ₂ - широты пунктов А и В; z₁ и z₂ - зенитные расстояния светила

Поскольку при таких вычислениях основной линейной единицей служит радиус Земли, его и считают в данной задаче базисом, в нем и выражают все линейные размеры. При определении расстояния до звезд базисом служит радиус земной орбиты. Измерив параллактическое смещение звезды и зная радиус земной орбиты, можно вычислить линейное расстояние до звезды в радиусах земной орбиты.

Действительно, в треугольнике ASB (рис. 27) углы SAB и SBA измеряют во время наблюдений звезды S, проводимых через полгода. А основание АВ этого треугольника равно диаметру земной орбиты. Отсюда несложно вычислить и расстояние до звезды.

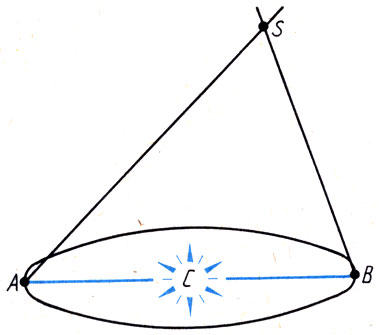
Рис. 27. Определение расстояния до звезд

Параллаксом звезды называется наибольший угол, под которым с нее был бы виден радиус земной орбиты (рис. 28). Это угол TSO в прямоугольном треугольнике, в котором гипотенуза OS есть расстояние от Солнца до звезды S, а малый катет ОТ - расстояние от Солнца до Земли.

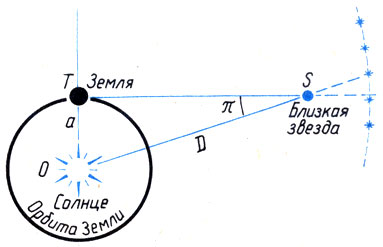
Рис. 28. Годичный параллакс звезды

Такие параллаксы называются годичными, так как они связаны с годичным обращением Земли вокруг Солнца. Годичные параллаксы даже ближайших звезд выражаются десятыми долями секунды дуги.

Масштабы расстоянии в мире небесных тел заставляют астрономов пользоваться гораздо более крупными единицами расстояний, чем километры. Приведем основные астрономические единицы расстояний.

1. Астрономическая единица (а. е.) равна среднему расстоянию от Земли до Солнца (≈ 149,5 млн. км).

2. Световой год (св. год) - расстояние, проходимое лучом света за год (за 31,5 млн. с со скоростью около 300 000 км/с). В световом году почти десять биллионов^* километров и более 60 000 а. е.

^* (Биллион - миллион миллионов (10¹² ). )

3. Парсек (пк) - расстояние, соответствующее параллаксу в 1": 1пк=3,26 св. года=206 265 а. е.= 3*10¹⁶ м.

В современной звездной астрономии пользуются парсеками, килопарсеками (кпк) и мегапарсеками (Мпк).

Зная расстояние до небесного тела и измерив его угловой радиус, т. е. угол, под которым с Земли виден радиус небесного тела, легко вычислить этот радиус в линейных единицах.

Из чертежа (рис. 29) видно, что R = Dsinα, где R - искомый радиус, α - угол, под которым он виден с Земли, a D - расстояние до данного небесного тела.

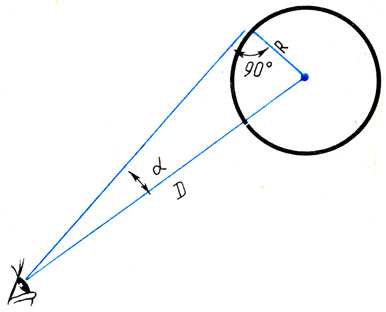
Рис. 29. Определение размеров небесных тел

Описанные методы определения расстояния до небесных тел и их размеров являются основными, хотя и не единственными. В истории астрономии они сыграли огромную роль, так как благодаря этим методам постепенно стали известными реальные размеры небесных тел и расстояния, разделяющие их.

Первые точные определения параллакса Луны провели в 1752 г. французские астрономы Ж. Лаланд и Н. Лакайль. Расстояние между пунктами наблюдений они старались выбрать как можно большее, чтобы параллактическое смещение Луны оказалось достаточно заметным. Лаланд измерял координаты Луны в Берлине, а Лакайль в тот же момент на мысе Доброй Надежды. Позже подобные измерения многократно повторялись, и по современным данным среднее расстояние до Луны близко к 400 000 км.

Первое надежное определение параллакса Солнца удалось выполнить французским астрономам Д. Кассини и Ж. Рише еще в 1672 г. Они получили для него значение, равное 9,5", в то время как на самом деле он составляет 8,79". Последняя величина была утверждена XII ассамблеей Международного астрономического союза в 1964 г. В 1976 г. были приняты следующие официальные значения главнейших астрономических постоянных:

 астрономическая единица................ 149 597 870 км
 скорость света......................... 299 792 458 м/с
 экваториальный радиус Земли............ 6 378 140 м
 наклон эклиптики к экватору............ 23°26'21"
 среднее расстояние от Земли до Луны.... 384 400 м 

Проделайте несложный эксперимент-поместите палец перед собой и поочередно посмотрите на него то правым, то левым глазом (закрывая при этом другой глаз). Вы сразу обнаружите, что ваш палец как бы "скачет" на фоне далеких предметов, испытывая кажущееся параллактическое смещение.

Причина параллактического смещения очевидна - вы смотрите на палец из разных точек пространства. Отодвиньте палец от лица - параллактическое смещение уменьшается. Следовательно, при прочих равных условиях оно зависит от расстояния до наблюдаемого предмета, убывая с возрастанием этого расстояния.

При движении Земли вокруг Солнца близкие звезды должны смещаться на фоне более далеких звезд. Параллактические смещения звезд совершаются по крошечным эллипсам тем меньшего размера, чем дальше от нас находится звезда. Кроме того, форма параллактического эллипса зависит от положения звезды по отношению к плоскости земной орбиты. В частности, звезды, лежащие в самой этой плоскости, очевидно, должны колебаться вдоль крошечного отрезка прямой - как бы полностью "сплющенного" эллипса. Во всех случаях, однако, параллактические смещения звезд, являющиеся своеобразным отражением орбитального движения Земли, имеют один и тот же период, равный году. Параллактические смещения звезд, в существовании которых был уверен еще Коперник, удалось обнаружить и измерить только в прошлом веке. Пионером в этом деле был уже знакомый нам основатель Пулковской обсерватории В. Я. Струве.

В феврале 1837 г. В. Я. Струве опубликовал результаты наблюдений, проведенных им на обсерватории Дерпта (Тарту) еще в 1835- 1836 гг. Струве старался измерить параллакс Веги - главной яркой звезды в созвездии Лиры. В итоге 17 наблюдений параллакс Веги получился равным 0,125"±0,055", что соответствует удалению на 26,5 св. года. Значение этого первого в истории измерения расстояния до звезд трудно переоценить. Оно не только показало человечеству масштабы звездного мира, но и окончательно, опытным путем подтвердило истинность системы Коперника.

После Струве и другим ученым удалось заметить параллактические смещения нескольких ближайших звезд. Как и следовало ожидать, они оказались исчезающе малыми. Из-за чрезвычайной удаленности звезд даже у самых близких из них наибольшие диаметры параллактических эллипсов не превышают одной секунды дуги. Под таким углом видна булавочная головка с расстояния 140 м! Неудивительно, что подобные углы, во времена Коперника измерить было невозможно,- лишь использование телескопов резко увеличило точность астрометрических измерений.

К сожалению, описанный метод тригонометрических параллаксов годен только для ближайших звезд. Дальнейшее продвижение в глубины звездного мира потребовало применения иных, астрофизических методов.