Земные заботы астрометрии

Астрометрия была рождена практическими нуждами человека, и неудивительно, что прикладной характер она сохранила до наших дней. В задачи практической астрономии входит прежде всего возможно более точное определение географических координат небесных светил и поправки часов, т.е. создание опорной системы координат, без которой немыслимо ориентироваться ни на небе, ни на земле. Решению этой проблемы сопутствует создание возможно более точной службы времени. Зная время и координаты небесных светил, можно решать чисто земные задачи - определять широту и долготу любого пункта земного шара и, как следствие, создавать всевозможные карты. Во .всем этом кровно заинтересованы не только мореплаватели, летчики, но и картографы и гебдезисты.

Широту места удастся найти, если измерить высоту звезды или другого светила с известным склонением в момент его верхней кульминации. Пусть эта кульминация происходит на участке небесного меридиана между южной частью горизонта и зенитом (т. е. к югу от зенита) (см. рис. 2), тогда h=90°-φ+δ, откуда φ= 90°-h+δ, или

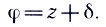
При кульминации звезды к северу от зенита можно вывести подобную формулу. Значит, измеряя зенитное расстояние z и зная δ, сразу находим широту места φ. И наоборот, зная z и φ, легко определить δ.

Как уже говорилось, на каждом географическом меридиане есть свое местное время (солнечное или звездное). На двух меридианах разница местных времен равна разности их географических долгот. Следовательно, зная местное время и время в Гринвиче^* (или другом пункте), легко найти долготу наблюдателя. Заметим, что местное время определяют по наблюдению звезд или Солнца. Как уже говорилось, местное звездное время в данный момент равно прямому восхождению кульминирующей звезды. Что же касается гринвичского времени, то раньше его "возили с собой" - брали хронометр, идущий по гринвичскому звездному времени. Теперь же подобную задачу решают проще, принимая специальные радиосигналы точного времени.

^* (В Гринвиче (Англия) находится одна из старейших обсерваторий, основанная в 1675 г. Принято отсчитывать долготы от Гринвича. )

Таков принцип. На практике все выглядит, конечно, сложнее. Приходится учитывать поправки часов, пользоваться таблицами для перевода звездного времени в солнечное или обратно и т. п.

На суше выполнять такие работы, естественно, легче, чем на качающейся палубе корабля или в кабине летящего самолета. Но и здесь вышли из положения, изобретя оригинальный угломерный инструмент - морской секстант. Идея его принадлежит И. Ньютону, а практическое осуществление - английскому механику начала XVIII в. Р. Гадлею. При измерении угловой высоты светила морской секстант держат в руке, и качка при этом не служит помехой. Разберемся в принципе действия этого замечательного инструмента. В секстанте (рис. 30) есть два плоских зеркала - неподвижное А и подвижное В. Когда луч S от светила после двукратного отражения от зеркал принимает направление АО, он попадает в глаз наблюдателя. Это направление составляет с первоначальным направлением луча угол SOA, вдвое больший угла АСВ между зеркалами. Из свойств треугольников следует:

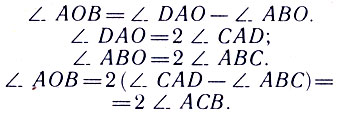
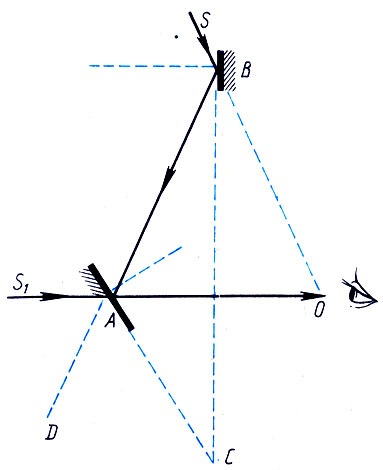
Рис. 30. Схема секстанта

Только половина стекла А покрыта металлом. Поэтому луч S₁, пройдя сквозь прозрачную часть стекла А, попадает в глаз наблюдателя по одному направлению с лучом S. Таким образом, если наблюдатель совмещает изображения лучей S и S₁ в своем глазу, то угол между ними вдвое больше угла между зеркалами.

Зеркало А крепится перпендикулярно к плоскости лимба, зеркало В закреплено на подвижной алидаде. При наблюдении лимб располагают в вертикальной плоскости и направляют зрительную трубу секстанта на линию горизонта. Вращая алидаду, добиваются того, чтобы светило "легло" на линию горизонта. В этот момент отсчет по лимбу дает угловую высоту светила. По высоте и склонению находят широту места, а долготу определяют так, как описано выше.

В авиационных секстантах вместо естественного морского горизонта его роль выполняет пузырьковый уровень, помещенный внутри инструмента. При наблюдениях авиаштурман совмещает изображение светила с изображением пузырька уровня.

Секстанты специальной конструкции используют и космонавты при работе в космосе. Измерения с секстантами, конечно, менее точны, чем, скажем, с универсальным инструментом. Но зато они просто и быстро позволяют ориентироваться в пространстве и во времени с приемлемой на практике точностью.

Без астрометрии, повторяем, мы не знали бы точной формы и размеров Земли, не имели бы карт, точного времени, а при путешествиях быстро потеряли бы правильное направление. Практическая значимость астрометрии не нуждается в доказательствах.