Крик новорожденного

Едва появившись на свет, еще не раскрыв свои глаза, малыш поднимает крик на всю округу. Ему жаль покинутого уютного местечка, а чудеса комфорта современного мира еще неизвестны.

Как появляется этот звук?

Вибрация эластичных голосовых связок вызывает колебания воздуха. Эти колебания излучаются ртом, распространяются в окружающей среде, и мы слышим крик малыша.

Раскрыв глаза, ребенок видит свет. Он воспринимает световые волны, поступающие от Солнца или лампочки. Так, не имея еще никаких понятий об окружающем мире, а тем более о колебаниях, ребенок рефлекторно излучает и принимает их.

Подрастая, этот молодой землянин будет сталкиваться все с новыми и новыми видами колебаний. Бросая камни в воду, он будет вызывать расходящиеся кругами волны. При этом далеко не всегда он будет следовать полезному совету Козьмы Пруткова: "Бросая в воду камешки, смотри на круги, ими образуемые; иначе такое бросание будет пустою забавою".

Раскачиваясь из стороны в сторону на макушке дерева (до чего здорово!), он совершает вместе с ним то нарастающие, то затухающие механические колебания.

Звонок об окончании урока временами ему будет казаться лучшей музыкой. Я до сих пор помню замирание сердца в ожидании этих спасительных звуковых колебаний в дни опросов. Часто выручало центральное положение буквы П. Но зато трепетать приходилось и при опросе "сверху" (с буквы А) и при опросе "снизу".

С электромагнитными колебаниями, или радиоволнами, молодая человеческая поросль теперь часто знакомится раньше, чем с букварем. Это заслуга домашних полуроботов - радиоприемников и телевизоров (третьи лица - родители - из этого процесса обычно самоустраняются).

Наконец, каждый человек имеет свой генератор ритмичных колебаний - сердце. Тысячелетиями даже мгновенная остановка этого генератора означала обрыв нити жизни. Последнее время человек в ряде случаев научился внешним толчком в несколько тысяч вольт снова пускать его в ход. Сделано несколько замен хлюпающего аритмичного генератора более молодым. Идет разработка миниатюрного генератора для подмены природного сработавшегося. Фразы "у него нет сердца", "у него холодное сердце" в недалеком будущем, наверное, будут звучать иначе - "у него транзисторное сердце".

Примеры встречающихся в природе и технике колебаний легко приумножить до сотен и тысяч. Но мы не пойдем, читатель, по этой тропе, поросшей скукой. Она ведь тоже мочалит наш источник колебаний. Нет ли компаса для ориентировки в этих джунглях колебаний?

Есть! Присмотримся к любому колебательному движению, например к колебаниям ног идущего или бегущего человека. Посылается правая вперед, левая остается сзади. Затем выбрасывается левая вперед, правая остается сзади (за счет перемещения тела). Что и есть один цикл колебаний. Значит, ходьба и бег есть результат простого периодического раскачивания противофазе двух маятников - ног, "закрепленных в одной точке". Чем больше циклов мы делаем в секунду тем большее пространство преодолеваем. Вот это число совершаемых циклов или колебаний в секунду и есть универсальный компас в мире колебаний. Имя его - частота колебаний.

Медленно гуляющий человек совершает, скажем, один цикл (два шага) в секунду. Такую частоту приняли за единицу и назвали герцем. Ноги спринтера колеблются значительно быстрее, и их частота достигает 15 - 20 герц.

Часто важно знать время, за которое совершается один цикл колебаний. Разделив одну секунду на частоту колебаний, мы получим эту величину: ее называют периодом колебаний.

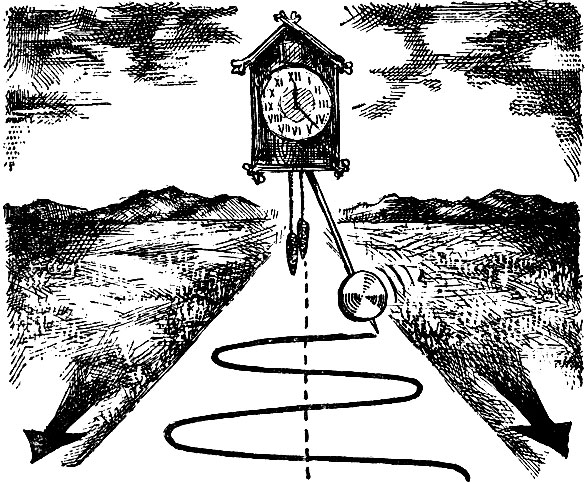
Рис. 20

Как-то я пытался выяснить у студента, куда движутся электроны в батарейке карманного фонаря: от плюса к минусу или наоборот. За 40 секунд нашего спора он ухитрился изменить свое мнение на обратное четыре раза. Средний период его колебаний "не так уж велик": T=40/4=10 секунд. Отсюда их частота F=0,1 герца.

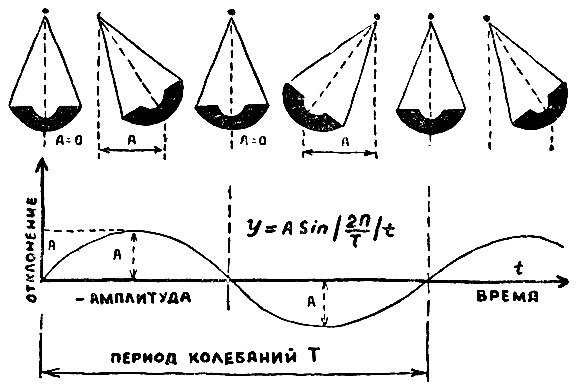
Рис. 21

Всякое движение, в том числе и колебательное, происходит во времени. Наблюдая положение или состояние колеблющегося тела в разные моменты времени, можно легко выявить периодичность и форму колебаний. Особенно наглядна их графическая запись. Проходя как-то мимо стройки, я увидел, что на ленте транспортера происходит запись некоего колебания. Вопли сверху открыли секрет. Ситуацию можно было назвать: "НОТ в действии". Маляр, развлекая свою очаровательную помощницу, раскачивал ее в люльке, как на качелях. С забытой кисти стекала краска. Она-то и отмечала положение качелей в разные моменты времени. На ленте мы видим волнообразную кривую, имеющую красивое, звучное имя - синусоида (вполне подходящее имя для гибкой, стройной девушки, не так ли?).

Синус обычно ассоциируется в сознании с треугольником. Мы с ним сталкиваемся в том или ином виде на протяжении всей жизни. Он же выражает временную зависимость отклонения маятника (качелей) от среднего положения. Поэтому колебания такого типа с характерным плавным переходом из одного крайнего состояния в другое получили название синусоидальных. Маляр и не подозревал, что совершает со своей спутницей путешествие по синусоиде. Максимальное отклонение качелей от нулевого положения называется амплитудой.

Колебания могут происходить не только по синусоиде.

Два примера. Электронный луч телевизионной трубки при развертке изображения совершает пилообразные колебания, похожие по форме на очертания зубьев пилы. Гейзер Великан (Камчатка) выбрасывает струю горячей воды в течение 4 минут, затем следует длительная пауза - 2 часа 55 минут. Амплитуда, или высота струи над поверхностью земли, достигает 40 метров. Такой режим работы называется импульсным, а его колебания - импульсными.

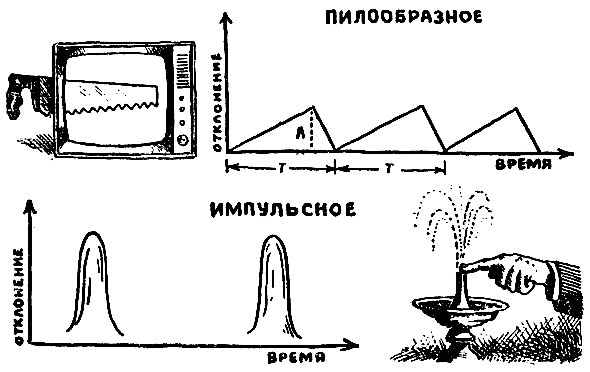
Рис. 22

Обратимся к вращательному движению. Здесь мы тоже наблюдаем циклические повторения. Есть ли это колебательное движение? Оказывается, сумма двух синусоидальных колебаний равной частоты, сдвинутых под углом в 90 градусов, образует круговое движение. Давайте подадим на вертикальные и горизонтальные пластины телевизионной трубки (или осциллографа) одно и то же синусоидальное напряжение. Это заставит электронный луч колебаться, как на качелях, одновременно и в вертикальной и в горизонтальной плоскости. На экране мы увидим неожиданный результат - идеально выписанную окружность.

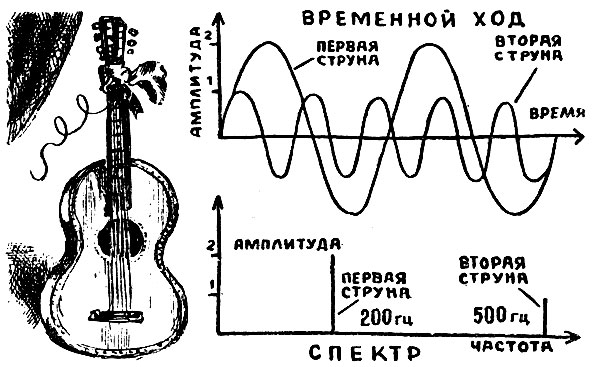
Рис. 23

Период вращательного движения, естественно, равен времени одного оборота.

Мы уже познакомились с разверткой колебаний во времени, или с его временным ходом. Имеется второй метод графического изображения колебаний. Он особенно удобен при изображении нескольких колебаний с разными частотами. При этом используется ось частот (а не ось времени, как в первом случае). На этой оси каждое колебание изображается вертикальной линией, высота которой пропорциональна амплитуде колебаний. Такое изображение получило название спектрального. Пусть две струны колеблются одновременно. Одна с частотой F₁=200 герц, другая с частотой F₂=500 герц. Амплитуда колебаний первой равна двум миллиметрам, а второй - одному миллиметру. Временной ход и спектр этих колебаний показан на приведенном здесь рисунке.

В природе и технике мы сталкиваемся с великим разнообразием колебаний. Поразительно то, что, меняя всего лишь один их параметр - частоту колебаний, мы меняем их свойства, их природу. Века потребовались человеку, чтобы распознать единую основу в морских волнах и солнечном свете, в звуках и радиоволнах.

Спектр изученных человеком колебаний очень широк.

Начинается он от очень медленных механических колебаний в доли герца и кончается невообразимо быстрыми рентгеновыми и гамма-лучами с частотой в миллионы миллиардов колебаний в секунду. А между ними сколько разных пород колебаний: звуковые, радиоволны, инфракрасные лучи, видимый свет, ультрафиолетовые лучи...

Таким образом, в наших колебательных джунглях скучать не будешь от однообразия видов.