Среди волн

Речь пойдет, конечно, не о восхитительной картине И. К. Айвазовского "Среди волн", почему-то недостаточно известной. Я как-то присел на минутку полюбоваться этим гигантским полотном, заполненным диким вихрем волн. Только волны. Кораблей нет. Людей нет. Берега нет. Только хаос возбужденной колебательной стихии. И не заметил, как провел у полотна два часа.

Что же такое волна?

Давайте выстроим шеренгу из старинных русских игрушек ванек-встанек. (Этот ванька обладает таинственной силой - нас так и тянет его валить и бесконечно наблюдать, как он бодро вскакивает.) Толкнем первого. Он начнет колебаться и передаст толчок второму, второй - третьему и т. д. Это простейшая модель преобразования колебаний источника в колебание, бегущее в пространстве. Такое распространяющееся в окружающей среде колебание образует волну. Почему она возникает?

Источник всегда окружен некоторой материальной средой. Возбуждающий элемент источника передает колебания непосредственно прилегающим к нему частицам среды. Они, в свою очередь, передают их своим соседям, более удаленным от источника, и т. д. Грубо говоря, генератор колебаний "раскачивает" окружающую среду, в ней возникают волны, распространяющиеся в этой среде. Частицы среды - лишь промежуточные ваньки-встаньки. Каждая из них колеблется, пользуясь модным словом, в своем микрорайоне. В этом легко убедиться. Ударьте пальцем по натянутой веревке. По ней побежит волна. Она передастся от элемента к элементу.

Меня много раз выручала эта волна в горах. Альпинистская веревка, часто называемая нитью жизни, имеет коварное свойство цепляться за все уступы, плохо лежащие камни и попадать в расщелины. Такое событие на трудной скальной стенке грозит печальными последствиями.

Но, пустив по веревке небольшую волну нужной амплитуды, удается освободить веревку и исключить опасность.

Следовательно, частицы среды не путешествуют вместе с волной. Именно благодаря этому световые и радиоволны преодолевают силы тяготения без всяких усилий, без всяких ракетных двигателей. Это и создает предпосылки для радиоконтактов.

Рис. 24

Из надписей на шкалах приемников познаются по крайней мере два факта:

- волны бывают разной длины (длинные, средние, короткие и ультракороткие);

- длина их обозначается греческой буквой А (лямбда).

Что же есть λ? Перенесемся мысленно на море. Плавая на морских волнах, вы чуть-чуть поссорились со своей подругой. Пребывание вместе на одном гребне волны стало принципиально невозможным. Ваша подруга переместилась на соседний гребень. Теперь расстояние между поссорившимися равно λ (при крупных ссорах дистанция в одну λ, вероятно, будет недостаточной). Итак λ - это расстояние, которое волна пробегает за время одного цикла или одного периода колебаний в среде, и называется длиной волны.

Подсчет λ прост: скорость распространения колебаний в данной среде надо умножить на время одного периода. По мере увеличения частоты длина волны, естественно, уменьшается.

Для радиоволн λ лежит в инвервале от сотен метров до долей сантиметра. Световые волны пробегают за время одного периода всего лишь одну миллионную долю сантиметра. А для гамма-лучей это расстояние нужно еще уменьшить в миллион раз!

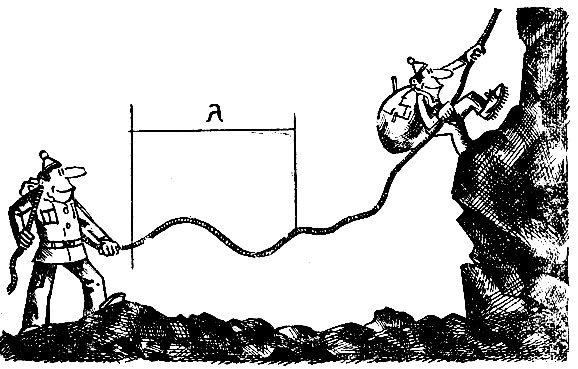
Рис. 25

Радиоволны настолько вошли в наш быт, что стали почти домашними животными. А ведь было время, когда только один человек на Земле верил в возможности излучения и распространения радиоволн. Этот человек создал общую теорию взаимодействия электрических и магнитных полей, выраженную им в строгой математической форме в виде уравнений.

Из уравнений следовал невероятный для того времени (1873 г.) вывод - можно создать радиоволны, которые будут распространяться на большие расстояния!

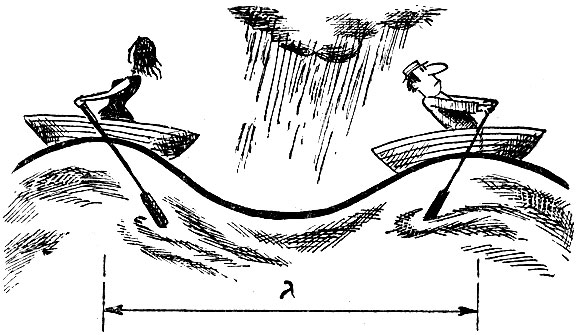
Рис. 26

Более того, уравнения позволили предсказать скорость распространения этих существовавших только на бумаге и в воображении ученого волн. Она оказалась весьма близкой к уже известной скорости света. Наконец, эти же уравнения вскрывали тайну световых лучей. Из них следовала электромагнитная природа света.

Кто же этот первооткрыватель радиомира? Это английский ученый Джемс Клерк Максвелл.

Спустя 15 лет существование радиоволн было подтверждено опытами, проведенными выдающимся немецким физиком Генрихом Герцем. Но сам он, как ни странно, не верил в будущее радиоволн. И понадобился гений Александра Степановича Попова, чтобы использовать волны Максвелла для передачи информации. Это случилось еще 8 лет спустя после опытов Герца - в 1895 году.

Полученные столетие назад уравнения, носящие название уравнений Максвелла, еще и сегодня являются стандартным аппаратом для анализа электромагнитных явлений в любых заданных условиях. Лучшими стихами на памятнике Максвеллу были бы... эти уравнения.

Чем же определяется предельная дальность распространения колебаний в среде?

Теоретически всякое колебание, раз возникнув в среде, распространяется в ней беспредельно, точнее, "достигает бесконечно удаленных точек с бесконечно малой амплитудой". Но из опыта мы знаем, что для всякого колебания (звукового, светового, радио) имеется предельное расстояние, за которым обнаружить его не удается.

В чем же дело? Не шутит ли с нами теория?

Ответ на этот вопрос читатель найдет в следующей главе.