§ 55. Определение радианта из односторонних наблюдений

Мы уже говорили о том, что для отыскания положения радианта надо найти точку пересечения двух метеорных траекторий. Для этого надо для каждой из них определить X и Y и написать уравнение большого круга (5.8). Точка пересечения (радиант) лежит на обоих кругах и, следовательно, решив оба уравнения совместно, можно определить координаты α_R и δ_R радианта. Однако эта задача не представляет интереса, так как радиант надо искать не путем такого решения по двум метеорам, а по совокупности траекторий нескольких метеоров.

Для определения радианта надо найти такую точку, которая была бы наименее удалена от каждой из траекторий метеоров, принадлежащих данному потоку. Таким образом, следует рассматривать величины Δ, определенные уравнением (5.9). Для этого надо сложить квадраты величин Δ и найти такие α_R и δ_R при которых сумма ΣΔ² имеет наименьшее значение. Это будет наивероятнейшим положением радианта.

Так как Δ - величины малые, то можно отыскивать Σsin²Δ, что гораздо удобнее. Воспользовавшись уравнением (5.9), мы сделаем в нем некоторые преобразования:

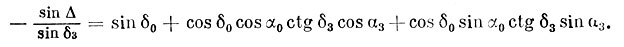
Для одного метеора это уравнение ничего не дает; величины α₃ и δ₃ в нем совершенно не известны. Однако для совокупности метеоров и таких уравнений α₃ и δ₃ получают совершенно определенный смысл - это координаты радианта. Если обозначить

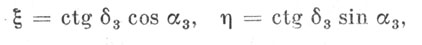
(5.10)

то система уравнений (5.9) примет вид

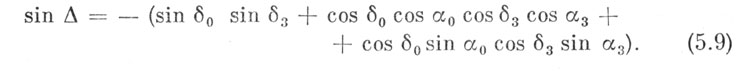
где i = 1, 2,..., n - поачислу метеоров; надо, отыскать такие значения ξ и η, при которых Σε_i² имеет наименьшее значение.

В Дополнении I (стр. 358) рассказано, что для этого надо сделать. Здесь мы дадим только краткие разъяснения.

Если бы все траектории метеоров, построенные наблюдателем, пересекались в одной точке - радианте, то все Af были бы равны нулю, и тогда уравнения (5.11) приняли бы строгий вид:

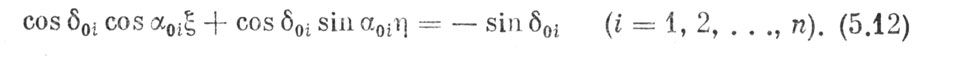
Так как этого нет, то каждое уравнение - не строгое и их принято называть условными, и всю систему уравнений решать по способу наименьших квадратов. Для этого составляются нормальные уравнения, которые в данном случае имеют такой вид:

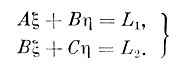
Здесь коэффициенты имеют следующий смысл:

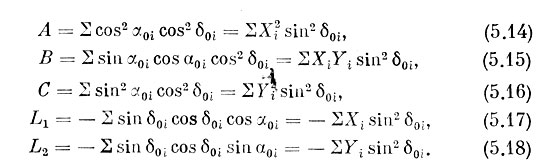
При преобразованиях мы воспользовались соотношениями (5.3). Таким образом, нормальные уравнения можно привести к виду

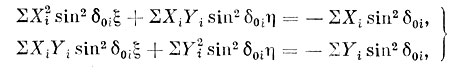
который показывает, что для получения численного вида нормальных уравнений лучше всего написать уравнения:

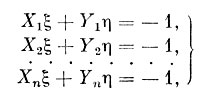
а затем умножить каждое из них на соответствующее ему значение sin δ_oi. Тогда получится такая система:

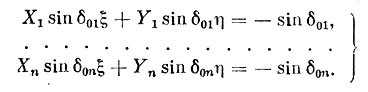
Суммируя квадраты коэффициентов по столбцам и их взаимные произведения между столбцами, мы автоматически получим нормальные уравнения в требуемой форме.

Решив нормальные уравнения, получим значения ξ и η, а затем значения α_R и δ_R из формул

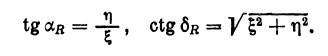
После получения решений надо обязательно проверить, правильно ли отобраны метеоры для объединения в одну систему условных уравнений. Для этого надо вычислить для каждого метеора его значение А. Это легко осуществить, использовав формулу (5.11), немного преобразовав ее к виду

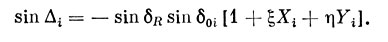
Способ наименьших квадратов позволяет также вычислить вероятные ошибки как величин ξ и η, так и α_R и δ_R

Заметим в заключение, что если какой-либо из метеоров даст значение Δ, большее допустимых пределов, то такой метеор надо исключить из обработки, так как он может принадлежать другому потоку. После исключения надо повторить все вычисления без него, что нетрудно сделать, зачеркнув одно из уравнений. Получатся более точные координаты радианта.

Описанный метод применим как к визуальным наблюдениям, так и к фотографическим. При этом надо заметить, что фотографические наблюдения, которые также доступны любителю (см. § 56), точнее визуальных и позволяют для каждой траектории определить исходные данные, Х_i и Y_i, гораздо точнее, по многим точкам, также по способу наименьших квадратов, а уже потом объединять данные о разных метеорах для определения радианта потока.