§ 56. Фотографические наблюдения метеоров

Фотографические наблюдения метеоров требуют применения светосильных, широкоугольных камер, высокочувствительных фотографических пластинок или пленок и могут проводиться только при темном фоне безлунного неба. Даже при этих условиях удается получать снимки только самых ярких метеоров. Однако из фотографических наблюдений можно получить гораздо более богатую информацию и потому их можно настоятельно рекомендовать. Эти наблюдения, вообще говоря, очень просты, так как наиболее точные результаты получаются при фотографировании неба неподвижными камерами, и для этого не надо параллактических установок и часового механизма.

Установив одну (или несколько, под различными углами) камеру, оставляем ее неподвижной. Тогда звезды в своем суточном движении будут давать изображения, перемещающиеся по эмульсии, и снимок будет покрыт совокупностью дуг -- изображений суточных параллелей. Изображение метеора выходит в виде более или менее длинной прямолинейной черты, пересекающей изображения суточных параллелей. На ней видны иногда вспышки (рис. 117).

Рис. 117. Снимок яркого метеора со вспышкой

Чтобы снимок можно было обработать, необходимо проделать следующее. Надо отметить по возможно более точным часам начало экспозиции Т₀ и ее конец Т_н. Кроме того, в процессе получения снимка надо через определенные промежутки времени (например, через каждые пять минут) закрывать непрозрачным экраном сразу все камеры на короткий срок (например, на минуту), записывая точные моменты закрытия и открытия. При этом никоим образом нельзя прикасаться к камере, чтобы не нарушить ее неподвижной установки. Обозначим эти моменты через Т₁, Т₁', Т₂, Т₂';... Эти перерывы в экспозиции приводят к образованию на изображениях суточных параллелей звезд белых просветов - «марок» времени.

Марки времени помогут нам определить прямые восхождения точек метеорной траектории.

Изображение метеора пересечет ряд суточных параллелей звезд. Мы будем определять координаты этих точек пересечения. Рассмотрим одно из пересечений, точку М (рис. 118).

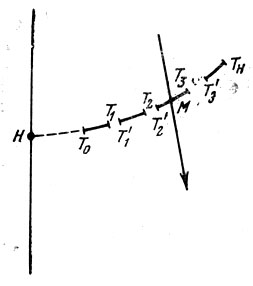
Рис. 118. Пересечнение изображения пути метеора (отмечен стрелкой) с изображением суточной параллели звезды (дуга)

Склонение точки пересечения определить очень просто: оно равно склонению той звезды, которой принадлежит изображение этой параллели. Сложнее определить прямое восхождение. Для этого находим ближайшие к точке М марки времени; на рис. 118 T₂' и Т₃. Измеряем на измерительном микроскопе, или, если его нет, на увеличенном при помощи проекционного фонаря изображении, расстояния T₂M = а и МТ₃ = b.

Если изобразить на рис. 118 дугу небесного меридиана, то, очевидно, часовой угол точки М, который мы обозначим через t_M должен измеряться дугой суточной параллели НМ. Так как моменты Т₂' и Т₃ нам известны, мы можем вычислить по ним звездное время s'₂ и s₃, а затем, зная прямое восхождение звезды α, найти по формуле t = s - α часовые углы марок времени t'₂ и t₃. Тогда часовой угол точки М вычислите я с достаточной точностью по формуле

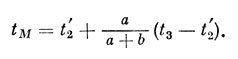
(5.24)

Теперь для отыскания прямого восхождения метеора необходимо знать момент, в который он пролетел. Снимок не дает возможности это сделать. Поэтому в самом начале, при организации фотографических наблюдений, надо обязательно организовать также визуальное патрулирование неба и отмечать на звездной карте пути всех пролетевших метеоров, записывая точные моменты времени полета метеора. Отыскав среди ярких метеоров тот, который был сфотографирован, мы узнаем точный момент времени Т_м, который нужен для дальнейших вычислений. По моменту Т_м находим звездное время s_м и вычисляем прямое восхождение α_м по той же формуле

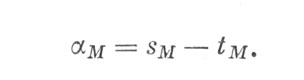
(5.25)

Приведем подробный пример. Метеорный снимок получен 12 августа 1962 г. Момент полета метеора, отождествленного на снимке, по всемирному времени 23 ч. 45 м. 13 с.

Изображение метеора пересекло суточную параллель α Лиры между марками T'_k = 23 ч. 10 м. 00 с. и Т_к+1 = 23 ч. 19 м. 00 с. в отношении а = 3,87 мм к b = 1,18 мм.

Приступаем к обработке. Выписываем из Каталога звездных положений координаты а Лиры; они отнесены к эпохе 1950,0 и надо учесть влияние прецессии и привести их к эпохе наблюдения, т. е. к моменту 1962 августа 12 = 1962,61 (здесь количество протекших дней с начала года превращено в десятичную дробь года). Выполнив эти преобразования по способу, описанному в §11, находим:

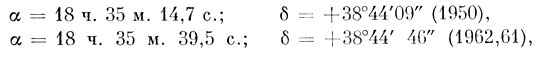
Итак, склонение точки М после округления равно δм = 38°44',8. Теперь приступим к определению прямого восхождения. Для этого прежде всего надо найти местное звездное время (см. § 16). Из Астрономического Календаря на 1962 год находим звездное время для 0 часов всемирного времени 12 августа:

s₀ = 21 ч. 19 м. 51 с.

Будем проводить все вычисления для трех моментов параллельно.

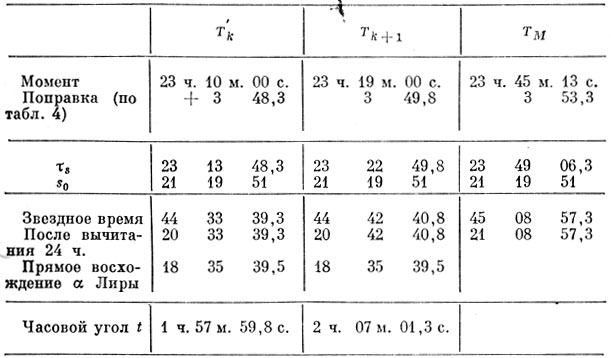
Вычисляем часовой угол точки М:

Для получения ам пользуемся формулой

α_м=s_м - t_м = 21 ч. 08 м. 57,3 с. - 2 ч. 04 м. 54,6 = 19 ч. 04 м. 02,7 с.

Итак, мы получили обе координаты точки М.

Получив совокупность пар чисел (α, δ), мы можем определить дугу большого круга, по которому летел метеор. Для этого надо воспользоваться уравнением (5.8), подставив в него известные α и δ. Тогда по данным каждой из точек можно написать условные уравнения (5.8) с неизвестными X и Y. Эти уравнения решаются по способу наименьших квадратов и определяются наивероятнешие значения X и Y. По ним с помощью формул (5.7) можно определить экваториальные координаты полюса траектории метеора.

При наличии совокупности нескольких метеоров можно использовать полученные значения X_k и У_k для определения координат радианта по формулам предыдущего параграфа. Как это сделать, показано на примере в § 57.

Наблюдения будут еще более ценными, если перед объективом установить быстро вращающийся обтюратор. Тогда можно определять и скорость полета метеора. Обтюратор - это прочный «пропеллер», укрепленный на вертикальной оси синхронного электромотора, число оборотов которого в секунду известно. Лопасти обтюратора должны быть настолько широкими, чтобы они полностью перекрывали объективы камер. Тогда, при вращении со скоростью 20-30 оборотов в секунду, на изображении метеора появятся перерывы. Измеряя координаты перерывов, можно определить угловую скорость метеора. Конечно, необходимо соблюдать технику безопасности, так как быстро вращающийся обтюратор может нанести серьезные повреждения наблюдателю.

Включение в установку обтюратора не снимает необходимости описанной выше маркировки звездных изображений. Поэтому надо приспособить укрепленную над обтюратором большую штору, которая перекрывала бы все камеры для нанесения марок времени, но управлялась бы дистанционно, с некоторого расстояния.