8.7. МАНЕВРИРОВАНИЕ

Маневрирование - преднамеренное изменение орбиты КА путем сообщения ему импульсов скорости.

Практически наиболее часто используются одноимпульсные маневры, которые удобно разбить на две группы: маневры с поворотом плоскости орбиты и маневры без изменения плоскости орбиты. Для рассмотрения свойств таких маневров предположим, что исходная орбита является круговой; это позволяет получить простые зависимости, в основном правильно описывающие и свойства эллиптических орбит, тем более, что обычные орбиты, как правило, являются слабоэллиптическими.

Положение плоскости орбиты будем определять долготой восходящего узла и наклонением плоскости орбиты к плоскости экватора i, а импульс, сообщенный КА, разложим на три взаимно перпендикулярные составляющие ΔV_т, ΔV_s и ΔV_w, из которых составляющая ΔV_т направлена параллельно вектору скорости КА, ΔV_s - вдоль радиуса-вектора, связывающего центр масс КА с центром Земли, a ΔV_w - перпендикулярно плоскости орбиты. Тогда изменения и i за один виток определятся формулами:

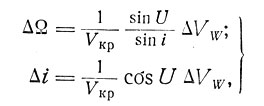
(8.10)

где V_kp - круговая скорость движения КА;

U - аргумент широты (угловое расстояние мгновенного положения КА от узла).

Из зависимостей (8.10) видно, что эффективность приложения к КА некоторого корректирующего импульса зависит от точки траектории, где этот импульс скорости сообщается КА (от координаты U).

Что касается порядков потребных значений импульсов скорости ΔVw, то, поскольку наибольшее возможное значение функций sinU и cosU равно единице, 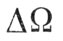и Δi будут иметь порядок ΔV_w/V_кp, т. е. Для поворота плоскости орбиты на один радиан (57°,3) потребуется ΔV_w порядка Vкр. Поворот плоскости орбиты всего на один угловой градус потребует приложения импульса ΔV_w=140 м/с, что указывает на крайнюю трудность поворота плоскости орбиты.

Рассмотрим теперь изменение наиболее существенных параметров движения КА, определяющих вид его траектории в плоскости орбиты. Ограничимся двумя величинами - параметром р, характеризующим линейные размеры орбиты, и эксцентриситетом в, характеризующим форму орбиты. При сделанных выше предположениях

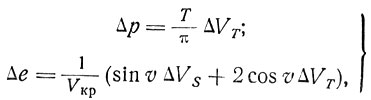
(8.11)

где Т - период обращения спутника вокруг Земли;

v - истинная аномалия (угловое расстояние от перигея до КА).

При Т = 90 мин Δp = 1700ΔV_т, т. е. изменение скорости движения на 1 м/с дает изменение размеров орбиты на 1,7 км. Это весьма эффективное приращение, так как обычные маневры (например, поддержания высоты полета) имеют порядок 100 - 200 км и требуют для этого сообщения КА скорости всего в 60 - 120 м/с. Что касается величины Δе, ее оценка по формулам (8.11) не имеет такой наглядности и более удобна при рассмотрении маневра, связанного с переходом на траекторию снижения в атмосфере, т. е. при рассмотрении посадочных импульсов.

Направление посадочного импульса может варьироваться в самых широких пределах. Рассмотрим свойства двух основных посадочных импульсов - импульса торможения и импульса «прижатия». Первый направлен против скорости орбитального движения и приводит к снижению скорости полета, второй направлен к центру Земли и приводит к повороту вектора скорости полета.

В качестве идеализированной схемы посадки примем такую, при которой в результате приложения к КА посадочного импульса первоначально круговая орбита деформируется и на некотором ее участке, соответствующем точке условного перигея (т. е. перигея, который образовался бы при отсутствии атмосферы), КА достигнет области, лежащей уже в достаточно плотных слоях атмосферы, сопротивление которой движению КА и приведет к посадке. Поэтому будем считать точку условного перигея точкой конца космического полета и судить о маневре посадки по этой точке.

Как известно, в точке перигея истинная аномалия = 0 и расстояние КА от центра Земли r = р/(1+e), тогда изменение высоты полета ΔH, соответствующее этой точке,

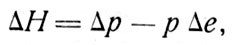
(8.12)

где Δр и Δе определяются по уравнениям (8.11), a v берется для точки сообщения КА посадочного импульса, а не для точки перигея.

Определение значения угла истинной аномалии v для точки, в которой КА сообщается посадочный импульс, затруднено тем, что у исходной круговой орбиты не существует перигея, от которого ведется отсчет v, но можно считать, что перигей образуется с первого же мгновения включения РД для маневра. В случае если КА сообщается импульс торможения, перигей образуется в противолежащей точке орбиты и, следовательно,. точке местонахождения КА будет соответствовать v=π, а в случае сообщения КА импульса «прижатия» перигей образуется на угловом расстоянии π/2 в направлении движения от точки приложения импульса, т. е. v = 3/2π. Подставляя эти значения в уравнения (8.11) с учетом равенства (8.12) и принимая за параметр орбиты р сумму радиуса Земли и обычной высоты полета, найдем, что на импульс в 1 м/с ДЯ = 3,2 км для импульса торможения и ΔH = 0,8 км для импульса «прижатия». Следовательно, импульс nорможения в 4 раза более экономичен, чем импульс «прижатия», однако последний имеет примерно вдвое меньшее время полета до посадки вследствие вдвое меньшего пути до точки условного перигея.

Таким образом, в околопланетном пространстве надо всячески избегать или сводить к минимуму маневры поворота плоскости орбиты, предпочитая им маневры в плоскости орбиты. Для примера рассмотрим маневр изменения периода обращения ИСЗ. Вследствие вращения Земли вокруг своей оси изменение периода обращения приведет к тому, что после такого изменения ИСЗ будет пролетать не над пунктами «исходной» орбиты, а над другими, новыми. Несложные выкладки для исходной круговой орбиты дадут

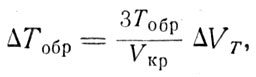
(8.1З)

где Т_обр - период обращения «исходной» орбиты.

Подстановка численных данных даст для обычных орбит ИСЗ изменение ΔТ_обр ≅ 2 с на импульс 1 м/с. Этой эффективности вполне достаточно для «подправки» орбиты так, чтобы снять неточности выведения КА или неточности, вызванные естественной эволюцией орбиты, и при необходимости пройти строго над заданным пунктом поверхности Земли без совершения маневра поворота плоскости орбиты.