Что значит задать орбиту

Собираясь в путешествие, вы назначаете свой маршрут движения, сообразуясь с рельефом местности, временем года и суток, наличием дорог, собственными силами, поклажей и многими другими факторами. Выбранный вами пешеходный маршрут может иметь причудливый вид, петлять, извиваться, огибать горы и озера, подниматься по склонам холмов и в живописных местах предусматривать остановки. Начертив на карте или чистом листе бумаги свой предполагаемый путь и отметив время прохождения его отдельных участков, вы можете с полным основанием утверждать, что задали свой маршрут. В процессе путешествия на отдельных отрезках пути вы можете идти быстрее или медленнее и это в принципе ничем не грозит вам, кроме как более поздним прибытием к конечному пункту.

Авиационные и морские штурманы прокладывают маршруты своих лайнеров по наикратчайшим расстояниям между пунктами, а время прибытия определяют по технической скорости движения лайнеров.

Этим самым они также задают свои маршруты движения. В отличие от маршрутов движения (пешеходам, автомобилям, тепловозам, морским судам и даже самолетам) для космических аппаратов задаются орбиты или траектории движения. Траектория движения - это совокупность последовательных 'положений аппарата, летящего в космическом пространстве. Если предположить, что траектория движения задана, то это значит, что нам дана сложная пространственная кривая линия, по которой будет двигаться космический аппарат. Представить ее в виде какой-то модели - сложное, а главное, бессмысленное дело, поскольку пользоваться ею на практике будет очень неудобно. Вот поэтому заданная траектория движения космических аппаратов не может быть показана так же просто, как маршруты движения для наземных средств передвижения, и имеет принципиальные особенности по сравнению с ним.

Первая особенность состоит в том, что все виды наземных средств (в том числе и авиационные) передвижения используют обязательно ту или иную опору - поверхность Земли, воду или воздушную среду. Поэтому, отталкиваясь от этой опоры, они в состоянии произвольным образом изменять маршрут своего движения, увеличивать или уменьшать скорость и даже делать преднамеренные остановки, совершенно не препятствующие дальнейшему путешествию. У космического аппарата нет такой опоры, и он летит по строго заданной траектории, определяемой условиями выхода на орбиту и последующим действием сил, опираться "а которые он уже не может.

Вторая особенность заключается в строгом лимитировании скорости его движения. Даже незначительное изменение скорости движения может привести к срыву всего полета и невыполнению поставленной задачи. Оказывается, что изменение скорости полета космического аппарата автоматически приводит к изменению траектории его движения, т. е. траектория и скорость глубоко связаны между собой и неразделимы. Конечно, такого явления мы не наблюдаем у наземных средств передвижения.

Как же тогда задать траекторию движения космического аппарата и чем она определяется?

Ha этот вопрос можно ответить следующим образом. Задайте своим приятелям такой вопрос: где вы были вчера? Одна часть из них может ответить примерно так:

- За городом в лесу.

- В кино.

- На рыбалке.

- На работе.

Другая часть, прежде чем ответить, переспросит: а в котором часу? Эта часть ваших приятелей более внимательна к постановке вопроса и ответу на него. Вчера - это сутки. В течение суток вы можете побывать во многих местах и поэтому ответ на поставленный вопрос может быть растяжимым: надо,, строго говоря, на каждый момент времени указать свое местоположение. Первая часть приятелей, видимо, имела в виду только лишь наиболее значительные для них события за истекший день, но гораздо меньше обращала внимание на пространственную сторону дела. Итак, когда мы задаем вопрос "где?" то ответом на него будет местоположение интересующего нас объекта в данный момент времени. Местоположение в геометрии, баллистике и вообще в математике определяется координатами объекта или отдельной точки его в определенной системе отсчета. Мы живем в трехмерном мире, или, как говорят, в пространстве трех измерений. Например, дом имеет определенную длину, ширину и высоту. Чтобы показать электромонтеру место, где вы желаете подвесить лампочку, вы можете указать точку на полу, над которой должна висеть лампочка (можно указать эту точку и прямо на потолке). Этим самым вы уже задали две координаты: точка на полу - это расстояния от двух пересекающихся стен. Третья координата - это высота лампочки над полом. В данном примере две пересекающиеся стены и пол являются системой отсчета координат всех предметов в комнате, в том числе и лампочки. Обобщая это понятие и распространяя на космические масштабы, точно так же вводятся системы координат для определения местоположения космических объектов. Одна из таких систем была упомянута ранее - это геоцентрическая невращающаяся система координат (рис. 12).

Вместо этой системы часто используют и так называемую гринвичскую систему координат. Все ее отличие от описанной системы состоит в том, что ось X, а следовательно, и ось Y уже не остается неподвижной в пространстве, а вращается вместе с Землей. Условились, чтобы эта ось проходила через гринвичский (нулевой) меридиан. Существуют и другие системы координат, о которых мы будем говорить позже.

Чтобы определить положение космического аппарата в этих системах координат (точно так же и в других прямоугольных системах), достаточно указать численные значения трех величин X, Y, Z. В процессе полета координаты X, Y, Z будут беспрерывно меняться, т. е. они являются функцией времени. Значит, когда мы указываем координаты космического аппарата, то одновременно должны приписать им определенное время. Отсчет времени - достаточно сложная отрасль астрономии и космической баллистики. Движение планет Солнечной системы, полет космического аппарата всегда рассматриваются во времени. В астрономических ежегодниках приводятся положения планет Солнечной системы относительно Земли, привязанные к строго определенным моментам времени. По времени мы находим координаты планет и, следовательно, действующее поле сил. Именно поэтому время является чрезвычайно важным признаком движения космического аппарата, поскольку оно определяет, с одной стороны, положение летящего аппарата над поверхностью Земли и, с другой, положение планет Солнечной системы, т. е. действующие силы. По этой причине на точность отсчета времени в космической баллистике налагаются очень жесткие требования. Например, баллистики совершенно не придут в восторг, если вы пообещаете измерять время с ошибкой в одну секунду. Они могут потребовать точность измерений порядка 0,01 сек, и даже еще выше.

Существует целая система отсчета времени. С ней вы можете познакомиться ниже.

Теперь мы обратимся еще к одной группе параметров, характеризующих движение космического аппарата, - его скорости. Скорость - векторная величина, т. е. она имеет строго определенное направление и величину. А это означает, что для того чтобы задать скорость движения, необходимо указать, во-первых, величину этой скорости и, во-вторых, направление ее. Направление скорости может быть задано углами относительно выбранной системы координат. Но чаще полные характеристики скорости удобнее задавать ее проекциями на оси координат. В этом случае вектор скорости V (рис. 16, а), содержащий в себе всю информацию о движении, т. е. направление и величину скорости, однозначно выразится заданием своих трех проекций на оси координат X, Y, Z, обозначаемых Vz, Vу, Vz. Часто эти проекции называют также компонентами вектора скорости, точно так же, как координаты X, Y, Z являются компонентами радиуса-вектора, указывающего местоположение космического аппарата (рис. 16).

Теперь мы можем ответить на поставленный вопрос - что значит задать орбиту:

задать орбиту космического аппарата - это значит указать три координаты и три компоненты скорости его в некоторый заданный момент времени.

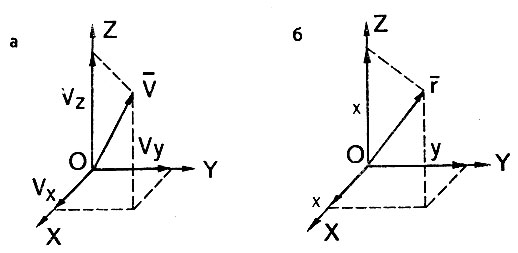
Рис. 16. Прямоугольные системы координат, определяющие местоположение (б) и скорость (а) полета космического аппарата

Таким образом, для задания орбиты движения аппарата необходимо назвать всего семь численных значений определенных величин, шесть из которых представляют кинематические параметры движения, а седьмая - время, к которому они отнесены. Перечисленные семь величин однозначно определяют последующий полет космического аппарата на все время его существования. Не правда ли, странно выглядит такое задание маршрута по сравнению с заданием его для всех видов наземных средств передвижения. Баллистики не рисуют свои орбиты, как это делают, например, летчики. В конечном счете при выборе орбиты они находят всего семь чисел и после этого утверждают, что если космический аппарат поместить в найденную точку и дать ему надлежащую скорость в заданное время, то он полетит именно туда, куда они этого желают.

Семь указанных чисел баллистики называют для краткости начальными условиями движения.

Нахождение начальных условий движения - сложное и трудоемкое дело. Баллистики встречаются с решением этой задачи в двух случаях.

В первом случае начальные условия движения находят при проектировании космических полетов, исходя из требований программы полета и его цели. Эти начальные условия называются номинальными, т. е. теми величинами, выполнение которых необходимо при выведении космического аппарата на орбиту. Процесс нахождения начальных условий чрезвычайно сложен. При решении этой задачи учитывают особенности конструкции космического аппарата, например, по возможности осуществления ориентации по небесным телам, по видимости космического аппарата с наземных пунктов, по минимальной затрате топлива на полет и т. д.

Во втором случае возникает задача определения фактических начальных условий движения, соответствующих действительной траектории полета. При подготовке к пуску система управления космического аппарата настраивается так, чтобы обеспечить выход его па номинальные условия полета. Например, для достижения Луны или планет Солнечной системы космический аппарат необходимо вывести к моменту окончания работы двигателя в строго определенную точку пространства над поверхностью Земли и сообщить ему точно рассчитанную по величине и направлению скорость. Однако из-за неизбежных ошибок работы системы управления, а также неточного знания действующих сил выход на орбиту всегда совершается с теми или иными отклонениями от номинальных начальных условий, которые могут существенно исказить траекторию последующего полета. Расчеты показывают, что при полете, например, на Луну в случае отклонения величины скорости в конце активного участка полета (на момент выключения двигателя) всего на несколько м/сек или отклонения направления скорости на десятую долю градуса от расчетных космический аппарат не попадет на Луну, а пролетит мимо. Таким образом, из-за влияния ошибок выведения траектория последующего полета будет отличаться от расчетной и, чтобы найти действительную траекторию, возникает необходимость провести измерения параметров движения космического аппарата и обработать результаты измерений математическими методами с целью определить фактические начальные условия. Когда в сообщении ТАСС мы читаем фразу "...координационно-вычислительный центр ведет обработку поступающей информации...", то именно одной из основных частей обработки информации является определение фактических начальных условий.

Выбор начальных условий движения - это процесс, по своему существу не новый даже в истории жизни человека древнейших времен. Вы, конечно, хорошо представляете себе стрельбу из лука или огнестрельного оружия. Стрелок из лука, если он желает к обеду подстрелить утку, в считанные секунды находит все необходимые начальные условия. Выбирая удобную позицию для стрельбы, он тем самым задает координаты, поворачивая лук в ту или иную сторону - направление стрельбы и по натяжению тетивы - величину скорости полета стрелы. И все это он ставит в соответствие с временем стрельбы. Правильно ли были найдены начальные условия, он определяет достаточно просто - по попаданию в утку. О фактических начальных условиях он судит по величине промаха. Конечно, это слабое утешение для изголодавшегося охотника.

Стрелок из ружья находится в лучших условиях, поскольку скорость вылета дроби из канала ствола ему задана и поэтому отпадает операция, аналогичная натягиванию тетивы.

Таким образом, мы рассмотрели вопрос о том, как задать орбиту движения космического аппарата. Предположим, что начальные условия движения нам известны. Как же после этого ответить на следующий вопрос - а куда полетит космический аппарат? Чтобы ответить на этот вопрос, разберемся вначале с формами задания начальных условий и системами счета времени.