Прогноз и теория эллиптического движения

В одном случае специалисты небесной механики нашли прекрасный заполнитель для "пустого ящика пана Юзефа" - это теорию эллиптического движения. Мы уже упоминали о ней, но сейчас остановимся более подробно. Эта теория возникла в результате решения следующей задачи. В космическом пространстве движутся две материальные точки, массы которых известны. Требуется определить траектории их движения, если они притягиваются друг к другу в соответствии с законом Ньютона. При этом предполагается, что действие каких-либо других сил, например, притяжение планет Солнечной системы, звезд, световое давление и т. д., отсутствует. Согласно изложенному ранее, вместо материальных точек можно рассматривать тела конечных размеров, имеющих ту же массу, но представленных в виде однородных шаров или сфер, поскольку их взаимное притяжение эквивалентно притяжению материальных точек. Понятно, что взятые условия задачи никогда (именно никогда!) в точности не выполняются на практике, поскольку, во-первых, ни одна из известных планет или каких-либо иных небесных тел не является в точности шаром и, во-вторых, кроме взаимного притяжения взятых тел на них еще действуют силы притяжения других тел. Следовательно, в такой формулировке задача носит идеализированный характер и уже поэтому мы не вправе безоговорочно применять ее для решения практических задач. Несмотря на это, результаты решения данной задачи находят широкое применение во многих прикладных вопросах и всякий уважающий себя баллистик никогда не пренебрегает ими.

Задача эта возникла не случайно. В природе можно найти множество примеров, когда условия задачи почти удовлетворяются. Например, движение электрона относительно ядра в атоме водорода; движение Венеры, Марса, Земли и других планет вокруг Солнца; вращение Луны вокруг Земли. Здесь слово "почти" надо понимать так, что в процессе движения определяющим является взаимное притяжение ядра и электрона,. Солнца и Венеры, Земли и Луны и т. д., то есть налицо явно выраженное притяжение двух тел, тогда как притяжение других тел является на много порядков меньше. Кроме того, по своей форме и структуре каждое из этих тел достаточно близко к однородным шарам и поэтому их можно приближенно рассматривать в виде материальных точек. Вот поэтому сформулированная задача имеет большой практический интерес.

Точно так же эта задача распространяется на движение космического аппарата относительно какой-либо планеты. В этом случае полагается, что гравитационное поле планеты является центральным, а космический аппарат представляется материальной точкой, причем масса его является бесконечно малой по сравнению с массой планеты.

Основные закономерности движения планет в центральном поле сил были открыты Кеплером в начале XVII века в результате анализа видимого движения Марса относительно Солнца. Применительно для космических аппаратов эти законы можно сформулировать следующим образом:

Первый закон Кеплера. Движение космического аппарата происходит по круговой, эллиптической, параболической или гиперболической орбите. Один из фокусов орбиты совпадает с центром небесного тела.

Второй закон Кеплера. Если из центра небесного тела провести радиус-вектор к космическому аппарату, то площадь, ометаемая радиусом-вектором в единицу времени в любой точке орбиты, есть величина постоянная.

Третий закон Кеплера. Квадраты периодов обращения двух космических аппаратов, движущихся по эллиптическим или круговым орбитам, относятся как кубы больших полуосей этих орбит.

Мы не будем заниматься математической формулировкой законов Кеплера, но дадим к ним некоторые пояснения, уточняющие геометрический и физический смыслы движения в центральном поле сил.

Из этих законов прежде всего следует, что орбита космического аппарата будет плоской в течение всего времени движения. Плоскость орбиты проходит через центр небесного тела и остается неподвижной в пространстве. Таким образом, если представить, что гравитационное поле Земли является центральным, то космический аппарат, выведенный на орбиту ее спутника, все время будет двигаться по одной и той же орбите, не изменяющей своей ориентации относительно звезд. Отсюда становится ясным смысл введения элементов орбиты - долготы узла Ω и наклонения i, поскольку они всегда остаются постоянными и характеризуют положение плоскости орбиты в пространстве (рис. 17).

Несмотря на общность законов, движение по каждой из орбит - круговой, эллиптической, параболической или гиперболической - имеет внешнее отличие, так же как и сами орбиты имеют различную форму.

Круговая орбита - наиболее простая из всех видов орбит. Центр ее совпадает с центром небесного тела. Нарисовать ее можно с помощью циркуля. Чтобы задать орбиту, достаточно указать ее радиус. Как будет показано ниже, радиус орбиты однозначно определит скорость движения по орбите и период обращения. Положение орбиты в пространстве задается двумя углами - долготой узла Ω, и наклонением i. Чтобы определить положение космического аппарата на орбите, необходимо указать величину угла u между линией восходящего узла и радиусом-вектором космического аппарата (рис. 17). Так задаются все элементы орбиты, причем существенно заметить, что все они, за исключением величины u, остаются постоянными. В этом, между прочим, состоит удобство задания начальных условий движения в виде элементов орбиты, а не в прямоугольных координатах. Прогноз движения по круговой орбите находится чрезвычайно просто: изменяя единственную величину - аргумент широты, получим последовательные местоположения космического аппарата, которые спустя виток будут повторяться. Круговое движение наиболее просто иллюстрирует второй закон Кеплера: радиус-вектор космического аппарата ввиду постоянной скорости его движения по орбите за один и тот же промежуток времени поворачивается на равные утлы, т. е. ометает равные площади.

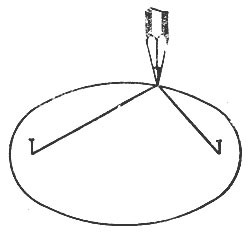
Рис. 18. Как начертить эллипс

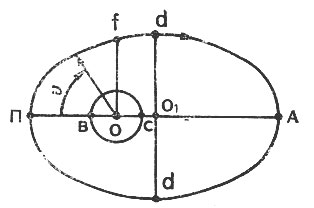
Рис. 19. Эллиптическая орбита

Эллиптическая орбита. Она напоминает сжатую с двух сторон окружность. Математически эллипс определяется следующим образом: это геометрическое место точек на плоскости, сумма расстояний которых от двух заданных точек есть величина постоянная. Нарисовать эллипс можно с помощью нехитрого приспособления. На листе фанеры вбейте два гвоздика (рис. 18) и к ним привяжите нить. Затем острием карандаша натяните нить и перемещайте его по бумаге вокруг гвоздиков, все время натягивая нить. Замкнутая кривая линия, которую нарисует карандаш, и будет являться эллипсом. Действительно, основания гвоздиков - это две заданные точки. Сумма расстояний от любой точки нарисованной кривой до гвоздиков будет одной и той же, поскольку используется одна и та же длина нити. Значит, это - эллипс. Те точки, в которые забиты гвоздики, называются фокусами эллипса. Первый закон Кеплера как раз и говорит о том, что при движении космического аппарата по эллиптической орбите вокруг небесного тела (т. е. по эллипсу) центр этого небесного тела будет совпадать с одним из фокусов.

На эллиптической орбите отмечают две характерные точки. Точка, наименее удаленная от центра небесного тела, носит общее название перицентр, а наиболее удаленная - апоцентр орбиты (на рис. 19 они обозначены буквами П и А соответственно). Очевидно, что эти точки лежат на прямой, проведенной через фокусы эллипса. Если в качестве небесного тела используется Земля, то для спутника Земли эти точки носят специфическое название перигея и апогея. В переводе с греческого это обозначает: перигей - возле Земли, апогей - от Земли. Для спутника Луны их обозначают периселений и апоселений (от слова Селена - Луна), для спутника Солнца - перигелий и афелий. В новых терминах вместо слова "ге" (Земля) использовано греческое слово "гелиос" (Солнце). Из сочетания слов "пери" и "гелиос" образовано "перигелий". Точно-так же сочетание слов "апо" и "гелиос" дало слово "афелий". Может показаться, что слово "афелий" возникло как-то иначе. Однако при его образовании в исходном слове была опущена буква о, а в получившемся слове aphelios сочетание ph произносится звуком, соответствующим русской букве "ф".

Термины "перигелий" и "афелий" применимы не только к орбитам космических аппаратов. Они относятся и к орбитам естественных спутников Солнца - планетам, кометам и астероидам. В последующем только для определенности мы будем, пользоваться терминами "перигей" и "апогей", имея в виду эллиптическую орбиту спутника Земли, хотя аналогичным образом мы могли говорить о спутниках Луны или Солнца и в этом случае пользоваться соответствующими обозначениями.

Расстояние от центра планеты до перигея (апогея) называют радиусом перигея (апогея). На рис. 19 они обозначены отрезками ОП и ОА. Расстояние от поверхности планеты до перигея (апогея), отсчитанное вдоль радиуса перигея (апогея), называется высотой перигея (апогея). На рис. 19 эти высоты обозначены отрезками вП и сА соответственно.

Вооружившись определением апогея и перигея орбиты, прочитаем следующий отрывок из сообщения ТАСС:

"...Параметры орбиты корабля "Союз-8" составляют:

- максимальная высота над поверхностью Земли (в апогее) - 223 км;

- минимальная высота над поверхностью Земли (в перигее) - 205 км;..."

Кажется, все ясно. Действительно, не вдаваясь в тонкости по этим величинам легко представить себе орбиту корабля "Союз-8". Можно согласиться с вами, что именно только представить, но совсем не определить строго. Вы спросите: а почему не строго, ведь определение апогея и перигея даны достаточно четко. Да, это так, но ответьте на следующие вопросы:

1. От какой поверхности Земли отсчитаны высоты апогея и перигея?

2. Высоты апогея и перигея были определены при движении космического аппарата по эллиптической орбите, то есть в центральном поле сил. Но поле Земли не является центральным и, следовательно, орбита корабля уже не будет эллипсом. Как же тогда понимать перигей и апогей?

Не огорчайтесь, если вы не в состоянии дать строгого ответа и пояснения к сообщению ТАСС. Даже опытный баллистик не в состоянии однозначно ответить на поставленные вопросы. Какие при этом могут быть варианты ответа, вы узнаете позже. А сейчас важно уяснить только одно, что сообщение ТАСС отражает близкую к истинной, достаточную для качественного представления, картину движения корабля "Союз-8".

Рисуя эллипс, можно брать различную длину нити, связывающей гвоздики. Чем короче будет нить, тем сильнее будет вытянут эллипс. Наоборот, при увеличении длины нити эллипс будет увеличиваться и по своей форме приближаться к окружности. Существует, следовательно, безграничное множество эллипсов, т. е. эллиптических орбит с одними и теми же фокусами. Размеры и форму эллиптической орбиты часто характеризуют ее полуосями - большой и малой. Большая полуось численно равна половине расстояния между апогеем и перигеем. Обычно она обозначается буквой а. На рис. 19 обозначено а = О₁ = О₁П. Малая полуось, обозначенная буквой b, на рис. 19 соответствует отрезкам O₁d. Для характеристики только формы эллипса, т. е. его вытянутости вводится безразмерная величина, которой дано специальное имя - эксцентриситет. Эксцентриситет - очень удобная величина для определения формы орбиты. Для эллиптических орбит эксцентриситет изменяется от 0 до 1, причем значения единицы не достигает. Чем больше значение эксцентриситета, тем значительнее вытянут эллипс. При е = 0 он обращается в окружность (в этом случае его полуоси равны, т. е. а = b, и оба фокуса совпадают). По мере приближения значения эксцентриситета к единице эллипс все более и более вытягивается (рис. 20). Забегая вперед, укажем, что при е = 1 он разрывается и превращается в параболу.

20. Формы орбит при различных эксцентриситетах: о - круговая; о<е><1 - эллиптическая; параболическая; е>1 - гиперболическая.

На эллиптической орбите часто выделяют еще одну геометрическую характеристику, называемую фокальным параметром и обозначаемую буквой р. Фокальный параметр - это расстояние вдоль перпендикуляра, опущенного к одному из фокусов, до точки пересечения с эллипсом. На рис. 19 один из таких параметров обозначен отрезком Of.

Таким образом, для характеристики формы и размеров эллипса имеется следующий набор величин: радиус апогея rа, радиус перигея rп большая полуось а, малая полуось b, фокальный параметр р, эксцентриситет е.

Для того чтобы математически описать эллиптическую орбиту, нет необходимости знать все перечисленные величины. Для этого достаточно знать только две любые из них, например, r_п, r_а, или а, е, или р, r_а и т. д. Значит, задавшись двумя из них, можно с помощью несложных математических операций найти остальные четыре. Формулы для таких пересчетов довольно просты и их можно найти в специальных книгах по небесной механике.

Положение космического аппарата на эллиптической орбите принято отсчитывать по угловому положению радиуса-вектора его относительно радиуса-вектора перигея в направлении? движения. Этот угол в небесной механике условились называть истинной аномалией и на рис. 19 он обозначен через О. Очевидно, что через каждый виток положение космического аппарата на орбите повторяется, т. е. прогноз движения рассчитывается достаточно просто.

Положение плоскости орбиты в пространстве задается точно так же, как и круговой орбиты, т. е. углами Ω и i (рис. 17).

Нам осталось указать последний элемент, характеризующий ориентацию орбиты в ее плоскости, поскольку она может быть произвольным образом повернута в своей плоскости вокруг фокуса, совпадающего с центром притягивающего тела. Таким элементом является аргумент широты перигея, обозначенный на рис. 17 через угол ω.

Таким образом, получены все шесть элементов (начальных условий), определяющих эллиптическое движение космического аппарата в пространстве:

а, е - характеризуют форму и размеры орбиты; Ω, i - положение плоскости орбиты в пространстве; υ - положение эллипса в плоскости орбиты; - положение космического аппарата на орбите. (Вместо величин а, е могли быть взяты другие комбинации элементов.) Если к этим элементам добавить время нахождения космического аппарата в какой-либо точке орбиты (т. е. при заданном значении истинной аномалии), то будем иметь полный набор исходных данных. Существенно еще раз отметить выгодность употребления элементов орбиты вместо прямоугольных координат. Пять из них - а, е, Ω, i, ω - являются постоянными и дают наглядное представление об орбите в пространстве и только одна - υ изменяется с течением времени. В то же время, если задать эллиптическую орбиту в прямоугольной системе координат, т. е. в виде трех координат и трех компонентов вектора скорости в заданный момент времени, то с течением времени наблюдалось бы изменение всех этих параметров движения и >по ним 'было бы трудно судить о характерах и свойствах движения.

Параболическая орбита. Ее уже нельзя нарисовать так же просто, как эллипс или окружность. Математическое определение параболы таково: это геометрическое место точек, разность расстояний которых от заданной точки и прямой есть величина постоянная. С видом параболы вы наверняка знакомы: брошенный вверх камень при своем движении описывает кривую, очень близкую к параболе.

Параболическую орбиту можно рассматривать как предельный случай эллиптической, когда расстояние между фокусами последней становится безгранично большим. Примерный вид параболы изображен на рис. 20. Точка ее, наименее удаленная от центра планеты, называется вершиной. Радиус-вектор вершины параболы служит началом отсчета истинной аномалии, указывающей положение космического аппарата на орбите, и точно так же, как радиус-вектор перигея в эллиптической орбите, служит для фиксирования положения параболы в ее плоскости.

Параболическая орбита является крайней из орбит, двигаясь по которой, космический аппарат может "оторваться" от планеты. Эта орбита наделена, если так можно выразиться, сугубо индивидуальными свойствами. Если космический аппарат, находящийся в вершине параболы, совершенно незначительно изменит величину скорости полета, он сразу же сойдет с нее. При уменьшении скорости орбита станет эллиптической, а при увеличении - гиперболической. При заданном радиусе вершины параболы скорость полета в этой точке строго и однозначно определена. Двух парабол, имеющих одну и ту же вершину, существовать не может. Совсем не то, что у эллиптических орбит: при заданном радиусе перигея их можно провести бесчисленное множество, изменяя, например, радиус апогея. Вот только по этой причине никогда не удавалось, да и наверняка никогда не получится выведение космического аппарата на строго параболическую орбиту.

Гиперболическая орбита хорошо известна в практике космических полетов. Начальные участки движения космических ракет, запускаемых к Венере, Марсу и другим планетам Солнечной системы, соответствуют именно гиперболическим орбитам.

По внешнему виду гиперболическую орбиту трудно отличить от параболической. Чтобы убедиться, что изображенная на некотором рисунке орбита является гиперболической, достаточно на нем нарисовать параболу с той же вершиной. Гиперболическая орбита охватывает параболическую (рис. 20) и ее эксцентриситет всегда больше единицы. Чем больше значение эксцентриситета, тем меньше вытянута гипербола и тем выше скорость движения по ней.

Фиксирование пространственного положения гиперболической орбиты и точки местонахождения космического аппарата на ней производится точно так же, как и в случае движения по параболической орбите.

Таковы основные виды орбит движения космического аппарата в центральном поле сил. В честь первооткрывателя законов движения их часто называют кеплеровыми орбитами. Иногда также встречается выражение: полет космического аппарата происходит по одной из кривых конического сечения. Это просто другое название кеплерового движения и причина его возникновения имеет простой геометрический смысл. Вам наверняка известна геометрическая фигура - прямой круговой конус. Если конус рассечь плоскостью перпендикулярно его оси, то в сечении получим окружность - круговую орбиту. Пересекая конус под некоторым углом к его оси, получим эллипс, т. е. эллиптическую орбиту. Увеличивая наклон плоскости, будем иметь все более и более вытянутые эллипсы, т. е. как бы моделировать увеличение эксцентриситета орбиты. Перемещение секущей плоскости параллельно самой себе даст в сечении эллипсы различных размеров, но с одним и тем же эксцентриситетом. Если секущую плоскость направить параллельно образующей конуса, то ее сечение конуса будет представлять собой параболу. Наконец, последующее увеличение угла между этой плоскостью и осью конуса даст в сечении гиперболу. Вот по этим причинам орбиты движения космического аппарата в центральном поле сил часто называют кривыми конического сечения.

Таким образом, аккуратно изготовленный из пластилина конус может явиться удобным средством для демонстрации видов орбит космического аппарата.

Расчет прогноза движения космического аппарата по кеплеровым орбитам выполняется чрезвычайно просто (по сравнению с численным интегрированием) с использованием конечных формул. С точки зрения количества вычислений здесь совершенно безразлично, на какое время рассчитывается прогноз - вперед на час, сутки, год или на какое-либо другое время и поэтому уже отпадает необходимость иметь для расчетов быстродействующие вычислительные средства (например, ЭВМ) с большой разрядной сеткой.

Однако теория эллиптического движения ввиду ее идеализированных предпосылок, как указывалось выше, пригодна лишь для качественного анализа движения. Чтобы учесть реальное поле сил, потребовалась большая и скрупулезная работа многих специалистов, однако и в этом направлении существует еще много неизученных "белых пятен", которые еще предстоит расшифровать.