Под притяжением Земли, Луны и Солнца

Мы уже не раз говорили, что нахождение траектории полета космического аппарата с учетом притяжения его Землей и Луной или Землей, Луной и Солнцем одновременно - до сих пор неразрешенная в аналитической форме задача даже при допущениях, что Земля, Луна и Солнце представляют собой материальные точки, совершающие полет по круговым орбитам. Чтобы все же как-то оценить влияние совместного действия сил притяжения двух или трех планет на летящий космический аппарат, баллистики пошли по старому, проторенному пути, в основе которого заложен метод теории возмущений. Напомним еще раз его существо. Представим, что космический аппарат выведен на орбиту спутника Земли, которая может быть круговой или эллиптической. В процессе полета на него будут действовать силы притяжения Земли, Луны и Солнца (притяжением других планет, очевидно, можно пренебречь, поскольку их влияние на много порядков меньше, чем притяжение Луны и Солнца). Однако для относительно низких орбит спутников Земли основную притягивающую силу будет создавать Земля. Количественный анализ максимальных значений соответствующих возмущающих ускорений, а также их отношений к ускорению земного притяжения в зависимости от высоты над поверхностью Земли показывает, что даже для орбит спутников высотой 100000 км возмущающее ускорение Луны и Солнца примерно в 10000 раз меньше земного ускорения и, таким образом, их отношение является очень малой величиной. Это обстоятельство дало возможность баллистикам учесть влияние притяжения Луны и Солнца следующим образом: они вначале рассматривают невозмущенный полет спутника (т. е. в поле притяжения одной Земли), а затем отыскивают малые поправки, обусловленные притяжением Луны и Солнца, к этому опорному невозмущенному движению. Конечно, найденное решение будет приближенным, но в принципе путем соответствующих математических операций (так называемых разложений в ряды) его можно сделать сколько угодно точным. Однако для целей качественного анализа, как правило, бывает достаточным первое приближенное решение, о котором говорят, что оно определяет главную линейную часть поправок. Если у вас возникнет желание более подробно познакомиться с математической стороной этого дела, вы можете обратиться к книге П. Е. Зльясберга "Введение в теорию полета искусственных спутников Земли".

Конечно, обсуждение вопросов возмущенного движения можно найти и в массе других книг и статей, но в книге П. Е. Эльясберга они изложены достаточно просто, понятно и последовательно.

Рис. 32. Схема действия Луны на движение спутника Земли: О - Земля; O1 - Луна; Д - спутник

Рассмотрим качественную сторону вопроса влияния возмущений на полет спутника от притяжения Луны и Солнца. Обратимся к рис. 32, на котором изображены положения Земли, Луны и спутника (точно так же может быть показано и положение Солнца). Точка O′₁ соответствует проекции положения центра масс Луны на плоскости орбиты спутника. Луна одновременно притягивает к себе как спутник, так и Землю, создавая ускорения A₁ и А₂, направленные к Луне. Значит, возмущающие влияния Луны на полет спутника проявляется в виде разности ускорений А₁ и А₂. Но нам уже известно, что величина ускорения, вызываемого силами притяжения, зависит от расстояния между притягивающими телами: чем больше это расстояние, тем ускорение меньше, и наоборот. Отсюда следует, что разность ускорений AB₁ и А₂, выступающая как возмущающее ускорение, будет наибольшей в том случае, когда расстояние от спутника и от Земли до Луны отличаются наиболее сильно. Такими точками на орбите спутника будут точки А₁ и А₂. В первом случае (при нахождении спутника в точке А₁) Луна станет сильнее ускорять спутник, чем Землю, и возмущающее ускорение будет направлено в сторону Луны. Во втором случае, когда спутник находится в точке А₂, ускорение Земли будет превышать ускорение спутника и поэтому возмущающее ускорение, - действующее на спутник, будет направлено от Луны. В этих точках будет наблюдаться более сильное по величине возмущающее ускорение. Во всех остальных положениях спутника оно будет иметь меньшее значение. Но ускорение - векторная величина и каждое из них, А₁ и А₂, будет всегда "следить" за положением Луны. Значит, результируюшее ускорение, выступающее как векторная разность ускорений А₁, и А₂, будет изменяться как по величине, так и по направлению, т. е. будет являться периодической функцией времени. В целях наглядности последующих рассуждений разложим результирующее ускорение на три направления - по нормали к плоскости орбиты (W), вдоль радиуса (S) и по перпендикуляру к радиусу-вектору в плоскости орбиты (Q) и теперь рассмотрим, как каждое из выделенных ускорений повлияет на орбиту полета спутника.

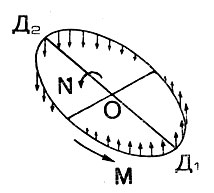
Рис. 33. Периодические возмущающие ускорения, действующие по нормали к плоскости орбиты

Влияние составляющей W. Типичный характер изменения этой составляющей вдоль орбиты спутника показан на рис. 33, где вертикальные стрелки обозначают возмущающие ускорения, стрелка М - направление полета спутника. Прямая Д₁Д₂ совпадает с линией проекции радиуса-вектора Луны на плоскость орбиты спутника. Очевидно, что если плоскость орбиты спутника будет совпадать с плоскостью орбиты Луны, то возмущающее ускорение W исчезнет и спутник будет все время двигаться в одной и той же плоскости. Когда же плоскости орбит не совпадают, то в одной части орбиты, приближенной к Луне, возмущающее ускорение будет направлено вверх, а в другой ее части, удаленной от Луны, оно будет действовать вниз. Что же произойдет в этом случае с орбитой спутника?

Когда спутник находится в окрестности точки Д₁ своей орбиты, то здесь возмущающее ускорение будет иметь наибольшее значение и его воздействие будет направлено на то, чтобы повернуть вектор скорости полета спутника вверх, т. е. в направлении, противоположном вращению часовой стрелки, если смотреть вдоль линии Д₁Д₂. Точно так же, когда спутник находится в окрестности точки Д₂, вектор скорости за счет влияния возмущающего ускорения будет также поворачиваться, отклоняясь вниз. Эти же эффекты, но уже в уменьшающейся степени, будут наблюдаться во всех других положениях спутника. Результирующее воздействие приводит к тому, что плоскость орбиты спутника начнет вращаться вокруг прямой Д₁Д₂ в направлении, указанном на рис. 33 стрелкой N.

Таким образом, итог воздействия притяжения Луны - вращение плоскости орбиты. По мере повышения Луны над плоскостью орбиты ее возмущающее влияние будет возрастать, но только до некоторых границ. Когда Луна окажется точно над центром орбиты вверху или внизу ее (что может быть достигнуто соответственным выбором условий выхода спутника на орбиту), то возмущающие ускорения во всех точках орбиты станут равными между собой и направлены в одну сторону, вследствие чего эффект поворота плоскости орбиты спутника исчезнет. Точный математический анализ показывает, что наибольшая скорость вращения плоскости орбиты будет наблюдаться в том случае, когда угол между плоскостью орбиты и направлением на Луну составляет 45°. Величина угла поворота плоскости за один виток спутника будет, очевидно, зависеть от радиуса или высоты его орбиты. С повышением орбиты притяжение Луны будет ощущаться сильнее. Соответствующие возмущения, обусловленные притяжением Солнца, будут примерно в 2,2 раза меньше. Однако процесс поворота плоскости орбиты из-за влияния Луны происходит значительно сложнее" чем просто последовательное повитковое суммирование поворотов. Дело осложняется тем, что одновременно с полетом спутника по своей орбите происходит и перемещение Луны вокруг Земли. В результате этого линия Д₁Д₂, на которую выпадает максимум боковых возмущений, будет постепенно, со скоростью одного оборота в один месяц для Луны и одного оборота за год для Солнца, смещаться вдоль орбиты. И, следуя за этой линией, автоматически сместится направление поворота плоскости орбиты. Все это значительно усложняет определение финального результата влияния возмущений Луны и Солнца. При этом не надо забывать и то обстоятельство, что в процессе вращения линии Д₁Д₂ одновременно может происходить снижение или повышение высоты Луны над орбитой спутника. Она может перейти с верхней стороны орбиты на нижнюю, в результате чего направление вращения плоскости орбиты спутника изменится на обратное.

Влияние составляющей S. Радиальная составляющая возмущающего ускорения от действия сил притяжения Луны слагается из двух частей - постоянной и периодической. Однако направление действий этих ускорений (т. е. от Земли или к Земле) и величина их существенным образом зависят от угла между плоскостью орбиты спутника и направления на Луну. В соответствии с этим наиболее интересны следующие три характерных случая.

Случай 1. Луна расположена на перпендикуляре к плоскости орбиты спутника. При нахождении спутника в любой точке своей орбиты Луна, притягивая к себе одновременно и спутник и Землю, будет стараться сблизить их между собой одним и тем же усилием. Иначе говоря, в этом случае спутник будет испытывать постоянное радиальное ускорение, равное во всех точках орбиты и направленное к центру Земли. Чтобы разобраться в качественном влиянии этого ускорения на последующий полет спутника, вспомним, что при отсутствии возмущающего ускорения спутник совершал полет по круговой орбите, в каждой точке которой центробежная сила и сила притяжения Земли находились в равновесии. Однако при наличии притяжения Луны возникнет новая сила (вызывающая возмущение движения), приложенная к спутнику и направленная к центру Земли. В результате равенство сил нарушится и спутник, .начав опускаться под действием возмущающей силы к Земле, станет увеличивать свою скорость. Увеличение скорости полета вызывает, в свою очередь, возрастание центробежной силы, которая уравновесит как силу притяжения Земли, так и возмущающую силу. Таким образом, воздействие радиального ускорения, обусловленного притяжением Луны, в конечном счете выльется в увеличение скорости полета спутника или в уменьшение периода его обращения. Этот эффект подтверждается строгим математическим анализом. В частности, при радиусе орбиты 100000 км период обращения спутника, равный примерно-4 суткам, уменьшится на 420 секунд.

Случай 2. Луна расположена под некоторым углом к плоскости орбиты спутника. Ввиду того, что Луна несколько отошла в сторону от перпендикуляра к плоскости орбиты и, следовательно, стала несколько ниже, то результирующее воздействие ее на спутник и Землю изменится. По мере приближения Луны к плоскости орбиты постоянная часть радиального возмущающего ускорения начнет уменьшаться и одновременно станет возрастать периодическая составляющая его. Математический анализ показывает, что когда угол между "плоскостью орбиты спутника и направлением на Луну станет равным примерно 35°, постоянная часть радиального ускорения исчезнет, а останется только периодическая (рис. 34). Эта составляющая в одних частях орбиты, будет стремиться вытянуть ее, а в других - сжать, соответственным образом периодически уменьшая или увеличивая скорость полета по орбите. В целом спутник будет колебаться около начальной орбиты, все время возвращаясь ,к ней, и вековых уходов его по периоду обращения или вдоль орбиты наблюдаться не будет.

Случай 3. При дальнейшем уменьшении угла между плоскостью орбиты и направлением на Луну постоянная часть возмущающего радиального ускорения сменит знак и будет уже воздействовать в направлении от центра Земли, как бы стремясь разорвать орбиту. Одновременно также будут возрастать и амплитуды периодической составляющей. Наибольших значений эти возмущения достигнут, когда Луна окажется в плоскости орбиты спутника (рис. 32). Преобладающая часть возмущений будет направлена от центра Земли и это в конечном счете (в силу указанных ранее причин) приведет к уменьшению скорости полета спутника и возрастанию периода его обращения.

Влияние составляющей Q. Эта составляющая ускорения носит также периодический характер и ее амплитуда зависит от высоты Луны над плоскостью орбиты спутника. Наибольшее значение это ускорение достигает, когда Луна лежит в плоскости орбиты спутника. Возмущающее ускорение Q, действующее в направлении скорости полета спутника или навстречу ей, приводит, как и в предыдущем случае, опять-таки к изменению периода обращения и смещению спутника вдоль орбиты, не вызывая каких-либо иных возмущений.

Для спутников, совершающих полет по круговым орбитам на высоте несколько тысяч километров и ниже, возмущения от притяжения Луны (и Солнца) являются пренебрежимо малыми. Однако на высотах порядка 20000 км они уже становятся заметными и при дальнейшем увеличении высоты полета резко возрастают и достигают значительных величин.

Следует заметить, что мы рассмотрели качественную картину эволюции орбиты спутника в наиболее простом случае, когда начальная орбита спутника круговая и действуют силы притяжения только Солнца или Луны. Приведенные результаты изменения параметров орбит оценивались только на первом витке после выведения спутника на орбиту, т. е. допускалось пренебрежение изменением их на движение по орбите. От витка к витку указанные возмущения будут все больше и больше нарастать, начальная круговая орбита потеряет свою форму, начнет все дальше деформироваться и сложным образом вращаться в пространстве. Отсюда сразу возникает вопрос - а каков будет финал движения, во что превратится орбита спутника и куда вообще спутник полетит? Может быть, что в течение всего времени он (если пренебречь влиянием сжатия Земли и сопротивлением атмосферы) будет как-то вращаться вокруг Земли, не удаляясь от нее за некоторые границы и не приближаясь к ней ниже определенной высоты? Или же рано или поздно вообще покинет Землю? А может быть, наоборот, упадет на нее? Вопрос этот чрезвычайно сложный. Баллистиками было сделано много попыток решить его в аналитической форме определенно и до конца, но выполнить это, к сожалению, до сих пор не удалось. А между тем этот вопрос имеет чрезвычайно важное значение. В будущем предполагается запускать специальные спутниковые станции с большим временем существования, измеряемым годами. Как же в этом случае ответить на вопрос - а на какую орбиту выводить их, чтобы возмущающие влияния Луны и Солнца "не испортили" орбиту? Если же большой деформации орбит все-таки исключить нельзя, то как из них выбрать те, которые в последующем потребуют минимальное количество топлива на их исправление? Как видим, поставленные вопросы имеют чисто прикладное практическое значение и они ждут своего решения.

А что можно сказать о влиянии притяжения Луны и Солнца на полет спутника по эллиптической орбите? Несомненно, решение этого вопроса сопряжено со значительно более высокими трудностями, чем в случае полета по круговой орбите. Качественная картина влияния возмущений здесь существенно усложняется и ее нельзя представить столь наглядной, как это было выполнено для круговой орбиты. Поэтому мы ограничимся только регистрацией основных выводов об особенностях движения.

Качественный анализ возмущающего влияния Солнца и Луны на движение искусственных спутников Земли показывает, что оно подвержено вековым возмущениям, пропорциональным времени полета и долгопериодическим солнечным и лунным возмущениям с периодом в половину месяца и в половину года. Кроме того, имеются короткопериодические возмущения с частотой, равной или кратной периоду обращения спутника.

Детальный анализ возмущенного движения показывает, что величины рассматриваемых возмущений целиком определяются размерами орбиты, наклонением ее плоскости, положением орбиты в этой плоскости, но в первом приближении не зависят от долготы восходящего узла. (При этом полагается, что наклонение плоскости орбиты, долгота узла и аргумент широты перигея определяются относительно вращающейся системы координат, связанной с положением возмущающего тела относительно Земли.) Величины возмущений, кроме того, в очень сильной степени зависят от размеров орбиты, в частности, от большой полуоси, изменяясь пропорционально кубу ее. Например, увеличение большой полуоси орбиты в два раза приводит к возрастанию вековых возмущений в 8 раз, но характер возмущений при этом не изменяется.

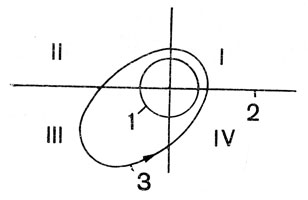
Рис. 35. Области понижения (I, III) и повышения (II, IV) высоты перигея: 1 - Земля; 2 - плоскость орбиты движения Луны относительно Земли (вид с ребра); 3 - одна из эллиптических орбит

Очень важный для практики интерес представляет собой вопрос об эволюции высоты перигея. Исследование этого вопроса показало, что вековое увеличение этой высоты имеет место при расположении перигея во второй или четвертой четвертях орбиты (рис. 35), а вековое понижение этой высоты - при расположении перигея в третьей или первой четверти орбиты. При этом максимум возмущений будет наблюдаться, если наклонение орбиты составляет 90° (к плоскости орбиты Луны или Солнца относительно Земли).

Наряду с этим будет наблюдаться вековое возмущение и других элементов орбиты. Орбита будет непрерывно изменять свою форму, одновременно сложным образом поворачиваясь в пространстве.

Параллельно с вековыми изменениями элементов орбиты спутника, пропорциональными числу оборотов спутника на орбите, будут иметь место так называемые долгопериодические колебания орбиты, связанные с вращением Луны и Солнца вокруг Земли. Эти возмущения носят фактически периодический (не вековой) характер и в течение каждого оборота Луны или Солнца достигают некоторых максимальных значений и затем снижаются до нуля. Наиболее существенную роль играют долгопериодические возмущения эксцентриситета и высоты перигея, так как возмущение этих величин имеет большое значение в решении ряда задач, связанных, например, с определением времени существования спутника.

Максимальные амплитуды рассматриваемых долгопериодических возмущений в основном определяются высотой апогея и слабо зависят от высоты перигея. Для спутников с высотой апогея более 100000 км максимальная амплитуда колебаний высот апогея и перигея достигает сотен километров.