Линии и поверхности Хилла

Конечно же, вопрос о финальном результате полета спутника Земли под влиянием притяжения Луны никак не может быть оставлен без внимания и изучение его, начавшееся со второй половины прошлого века, продолжается до сих пор. На современных известных исследований, посвященных этому вопросу, можно, например, выделить работу доктора физико-математических наук М. Л. Лядова "Эволюция орбит искусственных спутников планет под действием гравитационных, возмущений внешних тел". Мы также -пользовались известными результатами П. Е. Эльясберга. Эти, как и многие другие исследования, поставлены, если так можно выразиться, на инженерную точку зрения и позволяют дать четкий и однозначный ответ на вопрос об эволюции орбит спутников с максимальным учетом возмущающих сил не только от притяжения Луны, но и, скажем, сжатия Земли, притяжения Солнца и др. И в этом состоит величайшая ценность такого рода исследований, поскольку они направлены на решение именно практических задач, выдвигаемых самой жизнью. Однако в небесной механике известны иные, идеализированные пути решения, задачи - это определение областей движения материальной точки (в нашем понимании космического аппарата) в гравитационном поле Земли и Луны. Идеализированные предпосылки этой задачи состоят в том, что Земля и Луна представляются в виде материальных точек определенной массы, совершающих полет по круговым орбитам относительно общего для них центра. Это известная ограниченная задача трех тел. Мы уже упоминали, что решение ее в законченных аналитических соотношениях до сих пор еще не найдено. Но для нее известно одно соотношение, которое связывает в виде определенного равенства координаты и скорости космического аппарата в любой момент движения при данных начальных условиях. Это соотношение еще в прошлом веке было получено известным механиком и математиком Якоби и его обычно называют интегралом Якоби. Использование интеграла Якоби позволило американскому астроному Дж. В. Хиллу в своих исследованиях движения Луны (1877 год) выделить относительно Земли и Луны такие области, ограниченные определенными линиями и поверхностями, куда космический аппарат при заданных начальных условиях заведомо никогда попасть не может.

Поясним последнее обстоятельство. Мы уже говорили о том, что баллистиков очень часто волнует вопрос: куда в конце концов улетит космический аппарат, если на него одновременно действует притяжение Земли и Луны? Например, пусть спутник выведен на круговую орбиту с высотой 30000 км. Спрашивается, где он окажется, скажем, через месяц, через год, через 1000 или 1 000 000 лет, если пренебречь .притяжением Солнца, нецентральностью полей Луны и Земли и сопротивлением атмосферы? Вот именно этот вопрос и рассматривал в своих исследованиях Дж. В. Хилл. Правда, он не отвечает на вопрос - где конкретно будет находиться космический аппарат спустя определенное время полета, т. е. не называет определенную точку пространства его пребывания или какие-либо характеристики орбиты движения. Им указываются лишь области, в которых может находиться космический аппарат при заданных начальных условиях выведения на арбиту, и области, в которые спутник никогда не попадет, как бы долгим ни 'был его полет. Зная начальные условия, после несложных математических вычислений можно всегда установить область допустимых движений с помощью определенного критерия.

Линии Хилла удобнее всего рассматривать во вращающейся вместе с Землей и Луной системе координат. Поэтому и начальные условия движения необходимо задавать также в этой системе координат. Следуя Хиллу, отметим теперь наиболее характерные области возможных движений космического аппарата, полагая первоначально, что все три тела -- Луна, Земля и аппарат -- совершают полет в одной и той же плоскости.

Случай 1. Пусть начальные условия движения космического аппарата таковы, что он находится на очень большом расстоянии от центра масс системы Земля - Луна, исчисляемом многими сотнями тысяч километров, но имеет малую скорость полета, направленную в любую сторону. (Употребляемые нами обороты "очень большое расстояние", "малая скорость" не выражают точных границ рассматриваемого случая движения, а отражают лишь качественный характер начальных условий. Однако, как это уже указывалось, для них Хилл дает строго определенное значение некоторого критерия, о котором, не вдаваясь в область математических выкладок, здесь говорить не стоит.) Оказывается, что движение космического аппарата при любых начальных условиях, удовлетворяющих указанным ограничениям, может происходить в бесконечной во все стороны плоскости, за исключением заштрихованной на рис. 36, а области, ограниченной кривой, близкой по своей форме к окружности. Размеры этой области зависят от начального удаления космического аппарата от Земли и Луны - чем больше удаление, тем эта область шире. Вход в эту зону космическому аппарату "запрещен"; в лучшем случае он может просто коснуться ее или даже удержаться на ее краю, но войти внутрь никак не сможет. Законы небесной механики здесь выступают в роли неумолимого стража, не подпускающего к Земле и Луне космический аппарат ближе некоторого строго определенного расстояния. Но при этом космический аппарат совершенно не ограничен в свободе своего перемещения вне запретной зоны. Он может делать бесконечные петли вокруг "запретного плода", приближаясь, либо удаляясь от него, или навсегда покинуть его, чтобы больше никогда не возвращаться.

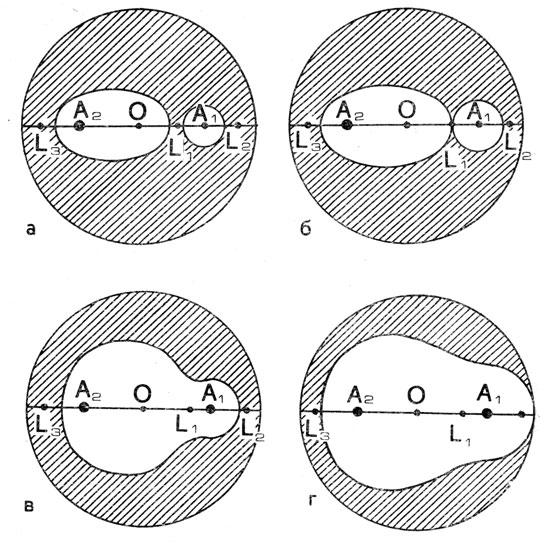
Рис. 36. Допустимые области движения космического аппарата в ограниченной круговой задаче трех тел. В заштрихованных областях полет космического аппарата 'запрещен'. А2 - Земля; А1 - Луна; А3 - точки либрации

Впрочем, такому характеру движения можно дать приближенное качественное объяснение. Когда космический аппарат находится на очень большом расстоянии от Земли и Луны, то приближенно можно считать, что Земля и Луна как бы представляют единый притягивающий центр с массой, равной сумме их масс. И для этой модели можно подобрать начальные условия движения, соответствующие круговой, эллиптической или гиперболической орбите. Они в последующем и определят характер движения космического аппарата относительно запретной области. Приведенные соображения будут, очевидно, тем ближе к истине, чем дальше в начальный момент находился космический аппарат от Земли и Луны.

Случай 2. Космический аппарат выведен на низкую (с высотой 200 - 300 км) круговую или слегка вытянутую эллиптическую орбиту спутника Земли. Анализ такого движения показывает, что, несмотря на постоянное возмущающее действие Луны, он никогда, ни через год, ни через столетие, ни через века, не выйдет из замкнутой вокруг Земли области, напоминающей собой овал (рис. 36, а). Размеры овала зависят от размеров начальной орбиты космического аппарата и определяются строгими математическими соотношениями по заданным начальным условиям движения. В течение всего времени полета космический аппарат, словно заключенный в клетку зверь, будет метаться внутри овала, "натыкаясь" на его границу, как на невидимую ограду, и "отскакивая" от нее. Природа построила довольно жесткое ограничение и оно может служить своеобразной тюрьмой для космических аппаратов. Точно такую же область можно выделить и для спутников Луны, только она будет скорее похожа на окружность. Необходимо отметить, что, находясь в этих областях, спутник все же не гарантирован от гибели: описывая самые хитроумные траектории, он может в конце концов столкнуться с Землей или Луной. Однако когда это произойдет - Хилл ответить не мог.

Случай 3. Начнем теперь постепенно увеличивать размеры орбит спутников Земли и Луны или увеличивать скорость их полета. В результате этого овал, описанный вокруг Земли, и близкая к окружности область вокруг Луны начнут увеличиваться в своих размерах, "разбухать" и при некоторых значениях начальных условий коснутся друг друга в точке Lt на линии, соединяющей Землю и Луну (рис. 36, б). Для спутника Земли, по-прежнему ограниченного в своем движении овалом, здесь появляется "лазейка" в точке L₁. Однако проскочить спутнику в эту лазейку не так-то просто. Первая сложность состоит в том, что ему необходимо попасть в нее, а для этого может потребоваться совершить колоссальное количество витков и петель внутри своей клетки. Вторая сложность обуславливается тем, что спутник подходит к "лазейке" всегда с нулевой (во вращающейся вместе с Землей и Луной системе координат) скоростью. Да, да, с нулевой. Какие бы он ни выписывал кривые, как бы ни метался внутри овала, с какой бы стороны он ни подходил к "лазейке", во всех случаях, достигнув ее, он остановится и будет покоиться, совершая полет вместе с точкой L₁. Но если после этого ему сообщить самую малую, микроскопическую скорость, как он тут же перескочит в область Луны и станет ее спутником. Точно так же обстоит дело и со спутником Луны.

Этот случай полета, как вы уже, наверное, догадались, является самым экономичным, с точки зрения расхода топлива, вариантом полета на Луну. Если стартовать с круговой орбиты спутника Земли высотой 200 км (а именно примерно с такой высоты стартуют космические корабли с целью полета к Луне), то скорость отлета космического корабля должна составлять 10848,90 м/сек. Достаточно уменьшить эту скорость на мизерную величину, например на 1 см/сек, как космический корабль уже никогда не достигнет Луны. Однако, стартуя с этой скоростью от Земли, не следует забывать, что если вы недостаточно точно прицелились и с первого захода не попали в "лазейку", то ваш корабль станет спутником Земли и неизвестно, сколько времени понадобится ему, чтобы он сам, без постороннего вмешательства, нашел потерянную лазейку. Но если даже вообразить, что вы, используя фантастически точные приборы, все же сумели проникнуть через "лазейку", то в дальнейшем полете едва ли будет легче: войдя в зону Луны, спутник начнет двигаться по совершенно неожиданной орбите, не отвечающей вашим намерениям. Вот по этим причинам запуск космических кораблей в сторону Луны с найденным ультраминимальным значением скорости производить нерационально. Выход из этого положения - увеличение начальной скорости. Но об этом мы будем говорить позже.

Найденная "лазейка" - точка L₁ - в небесной механике носит название точки либрации (как мы увидим впоследствии, таких точек в системе Земля - Луна существует несколько). Она имеет строго определенное положение - при расстоянии между центрами Земли и Луны 384000 км точка либрации L₁ находится на расстоянии 58000 км в направлении к Земле. Местоположение этой точки обладает любопытным свойством: тело, помещенное в эту точку, будет двигаться вместе с ней до тех пор, пока не подействует малейшая возмущающая сила. Даже небольшое возмущение выведет это тело из равновесного положения и оно начнет двигаться либо к Земле, либо к Луне, в зависимости от направления действия возмущения. Значит, точка либрации L₁ - точка неустойчивого равновесия. Положение этой точки на линии Земля - Луна или какой-либо другой пары планет вы можете легко найти и сами: она определяется тем, что действующие на точку силы притяжения планет уравновешиваются центробежной силой при вращении ее вместе с планетами относительно общего для них центра масс.

Случай 4. Дальнейшее увеличение скорости полета спутника (свыше 10848,90 м/сек при старте с орбиты спутника Земли, высота которой равна 200 км) или размеров орбиты расширяет область допустимых движений его и она принимает в 'плане вид гантели с неравными грузами на концах (рис. 36, в). "Лазейка" для спутника расширяется и превращается в широкий коридор. Движение спутника будет происходить внутри описанной области; он может побывать у Луны и, обогнув ее, вернуться к Земле, а затем, сделав несколько оборотов вокруг Земли, снова отправиться к Луне. Словом, единственное, что можно утверждать, так это то, что спутник не выйдет из заданной области, но где будет находиться в каждый конкретный момент - неизвестно. Последующее увеличение (Начальной скорости полета приведет к еще большему "разбуханию" гантели и она своим меньшим "грузом" коснется внешней границы запретной зоны в точке либрации (рис. 36, г). Здесь возникает ситуация, аналогичная только что описанному случаю, а именно: у космического аппарата появляется новая "лазейка", проникнув через которую он может выйти за внешнюю границу и навсегда покинуть Землю. Чтобы достигнуть этой "лазейки", спутнику Земли, стартующему с высоты 200 км, необходимо придать скорость 10849,68 м/сек, которая всего лишь на 78 см/сек больше скорости достижения точки L₁. Значит, увеличение скорости старта на столь мизерную величину позволит в принципе спутнику улететь от Земли и от Луны. Конечно, в силу указанных ранее причин отлетать от Земли в беспредельное звездное пространство через "лазейку" в точке L₂ практически невозможно, хотя бы потому, что никакая система управления ракетой не позволит получить столь высокие точности выведения. Однако даже относительно небольшое увеличение скорости полета всего на каких-нибудь 10 - 20 м/сек позволит совершить уверенный отлет от Земли со значительно менее жесткими требованиями к точности функционирования системы управления.

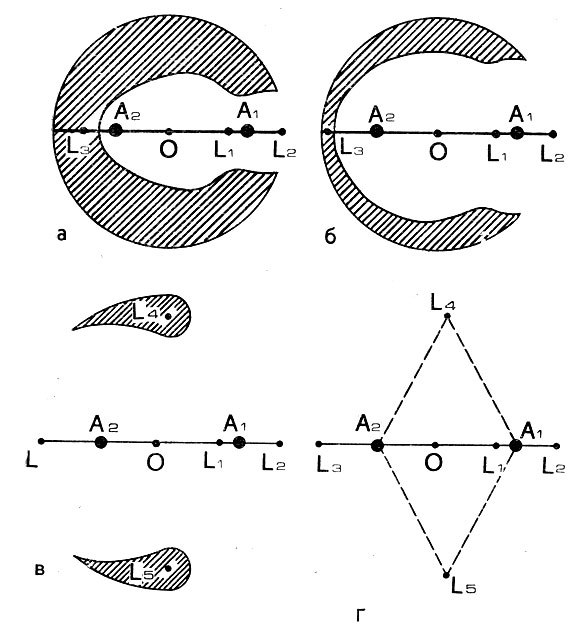
Рис. 37. Сужение 'запрещенных' (заштриховано) областей движения космического аппарата при увеличении начальной скорости полета

Точка L₂ - это новая точка либрации. Помещенное в ней тело будет все время находиться в ней, пока на него не подействует возмущающая сила, после чего тело либо уйдет в область гантели, либо в наружную область. В точке L₂ силы притяжения Земли и Луны, как и для точки L₁, уравновешиваются центробежной силой. Точка L₂ расположена на расстоянии 65 000 км от Луны.

Случай 5. Последующее увеличение скорости полета приводит к расширению области допустимых движений спутника. Вместо узкой "лазейки" в точке L₂ образуется широкое горло (рис. 37, а), сквозь которое спутник уже легче выйдет наружу и покинет Землю. Правда, это не исключает и того, что он, совершив прогулку в космосе, снова войдет в горло и станет обращаться в компании с Луной и Землей. Наступит, наконец, такой момент, когда возрастание скорости полета спутника при старте его с орбиты спутника Земли (или Луны) приведет к смыканию внутренней и внешней областей допустимых движений спутника слева от Земли в точке L₃ (рис. 37, б). Это третья точка либрации, аналогичная точке L₂. Для ее достижения ракета должна разогнать спутник до скорости 10857,38 м/сек. Если спутник угадает в эти "новые ворота", то он может покинуть Землю, не пролетая мимо Луны. Эти "ворота" расположены на расстоянии 380600 км от Земли. Но, как мы уже говорили, лететь через такие ворота невыгодно, поскольку требуется крайне высокая точность работы системы управления.

Три указанные точки L₁, L₂, L₃ - это так называемые прямолинейные точки либрации, поскольку они расположены на одной и той же прямой, проведенной через центры Земли и Луны. Общая характеристика для них - неустойчивость положения находящихся в них тел. В реальной системе Земля - Луна - Солнце без использования специальных корректирующих двигательных установок в них нельзя удержать космический аппарат. Правда, для поддержания искусственного равновесия потребуются небольшие ускорения, и в этом, может быть, заключается заманчивая идея использования этих точек для решения практических задач.

Случай 6. При дальнейшем нарастании начальной скорости горловина у точки либрации L3 (как, впрочем, и у точки L₂) будет расширяться, а области, не доступные спутнику ни при каком направлении начальной скорости, будут сжиматься (рис. 37, в). Спутник может удалиться от Земли практически по любому направлению, поскольку запретные для него области все более и более сжимаются. Наконец, когда скорость спутника на орбите около Земли с высотой 200 км достигнет 10858,54 м/сек, эти запретные области сожмутся в точки L₄, L₅, называемые треугольными точками либрации. Ввиду особых свойств этих точек остановимся на них несколько подробнее.

Местоположение точек либрации L₄ и L₅ найти очень просто. Они всегда лежат в плоскости орбиты движения Луны относительно Земли и образуют с центрами Луны и Земли равносторонние треугольники (рис. 37, г). В процессе вращения Земли и Луны относительно общего для них центра масс равносторонние треугольники, в вершинах которых расположены точки либрации, тоже вращаются вместе с этими телами. Подробный математический анализ выявил одну чрезвычайно любопытную особенность этих точек: они являются устойчивыми. Иначе говоря, если космический аппарат расположен не в самой точке L₄ (или L₅), а на некотором небольшом расстоянии от нее и имеет относительно этой точки небольшую скорость, то с течением времени он никуда не уйдет от точки либрации, а будет двигаться в некоторой окрестности ее.

Еще до недавнего времени изучение движения в окрестности устойчивых точек либрации носило чисто теоретический интерес, на основании которого было сделано предположение, что вблизи этих точек в системе Земля - Луна также скапливаются какие-то космические тела. Высказанное предположение подтвердилось: в марте - апреле 1961 года астроном Краковской обсерватории К. Кордилевский после многолетних поисков обнаружил два космических "облака", по-видимому, состоящих из метеорной пыли, в районе точки либрации L4. Через некоторое время подобные "облака" им были найдены в районе точки либрации L5.

Независимо от существования естественных объектов в окрестности устойчивых точек либрации возможен также вывод искусственных тел, космических аппаратов или станций, причем такая задача во многих чертах будет сходна с задачей перелета на орбиту спутника Луны. В обоих случаях космическому аппарату сначала сообщается скорость, необходимая для достижения желаемой точки, после чего осуществляется торможение с целью обеспечения "захвата".

Космический аппарат, помещенный в одну из точек либрации, может быть использован для ряда целей. Одна из целей - уточнение отношения масс Земли и Луны по наблюдениям движения такого космического аппарата с Земли. Это утверждение основывается на том, что периодичность движения его будет зависеть только от отношения масс Земли и Луны. Другая цель заключается в том, что космический аппарат, расположенный достаточно далеко от Земли и Лупы, может быть исползован для изучения солнечной и космической радиации или как ретранслятор при осуществлении радиотелефонной и телевизионной связи между отдельными пунктами на Земле.

Другие возможности использования космических аппаратов, помещенных в устойчивые точки либрации, заключаются в том, что они могут служить в качестве промежуточных станций при дальних перелетах и для изучения Земли. Часто для этой цели предлагают использовать Луну. Но ввиду отсутствия тяготения в точке либрации потребуются меньшие расходы топлива для остановки пролетающего корабля или, наоборот, отлета его, чем на Луне.

Но самые любопытные возможности применения точек либрации - устройство в них космических "складов". Ввиду их устойчивого положения в системе Земля - Луна здесь можно поместить и сохранить "на веки вечные" любые материальные тела без риска, что их зальет вода, засыплет песок, разрушит ветер или размоет дождь. "Стены" такого склада "никогда не обвалятся и не сгниют". В них - "абсолютная" тишина. Ни ветра, ни бури, ни окисляющего влияния атмосферы или воды. Эти склады никогда нельзя потерять, их положение надежно защищается и контролируется законами небесной механики. В то же время, даже на современном уровне развития ракетной техники, не представляет труда достичь этих точек и вернуться на Землю.

Точки либрации были предсказаны Лагранжем еще в 1772 году, но понадобилось целых 100 лет, чтобы подтвердить их существование в Солнечной системе. Астрономы нашли, к своему великому изумлению и радости, что точки L4 и L5 действительно имеются в Солнечной системе: в точках либрации системы Солнца - Юпитер были обнаружены двенадцать небольших астероидов, составляющих так называемую Троянскую группу и движущихся по орбите Юпитера на расстоянии 60° по обе стороны от планеты (рис. 38). Однако мы немного отвлеклись от основной темы нашего повествования - определения допустимых областей полета космического аппарата в поле совместного действия Земли и Луны. Это было сделано "е напрасно, ибо лишний раз свидетельствует о том, сколь большое значение для практики имеет теория. С одной стороны, она помогает объяснить непонятные до некоторых пор явления природы (например, расположение Троянской группы в Солнечной системе было бы трудно объяснить без знания точек либрации) и, с другой, способствует использованию новых закономерностей для решения практических потребностей космонавтики.

Мы достаточно подробно рассмотрели качественный характер движения космического аппарата в поле Земли и Луны и указали характерные области "разрешенных" и "запретных" ему движений в плоскости орбиты движения Луны относительно Земли. Пространственная структура этих областей, конечно, усложнится. Не вдаваясь во все тонкости дела, укажем лишь только наиболее примечательные из них.

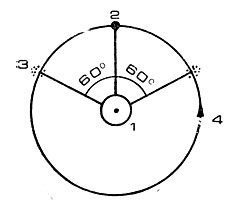
Рис. 38. Троянская группа астероидов в точках либрации L4, L5 системы Солнце - Юпитер: 1 - Солнце; 2 - Юпитер; 3 - астероиды; 4 - орбита Юпитера

Рис. 39. Область допустимых движений космического аппарата при больших удалениях от системы Земля - Луна

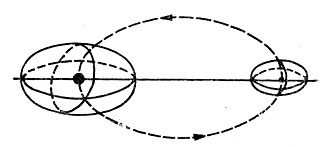
Рис. 40. Пространственные области допустимых движений спутников Земли и Луны

При больших начальных удалениях космического аппарата от системы Земля - Луна (им соответствует описанный случай 1) областью допустимых движений является внутренняя и наружная часть открытого с обоих концов цилиндра, имеющего в своей середине двояковыпуклую перегородку (рис. 39). Цилиндр этот должен быть неограниченно продолжен в обе стороны от плоскости орбиты движения Луны, причем по мере удаления "толщина стенок" цилиндра должна уменьшаться.

Если космический аппарат выведен на близкую орбиту спутника Земли или Луны, то допустимые области будут иметь вид овалов (рис. 40). По мере возрастания начальной скорости эти овалы начнут "разбухать" и при некотором значении ее коснутся друг друга в первой точке либрации. В дальнейшем овалы превратятся в гантель с неравными грузами на концах. Расширяясь, гантель вначале коснется своим малым концом поверхности цилиндра во второй точке, а затем большим концом - в третьей точке. Границы таких цилиндров, овалов и галтелей образуют упоминавшиеся ранее поверхности Хилла.

Линии и поверхности Хилла дают возможность хотя бы приближенно представить себе области возможных движений спутников при заданных значениях начальных условий. Чтобы найти окончательный, точный вид этих областей, необходимо условия полета спутника приблизить к реальным. Для этого, в частности, необходимо добавить притяжение Солнца, Луну заставить двигаться вокруг Земли не по кругу, а по слегка вытянутому эллипсу, Землю немного сжать с полюсов, после этого добавить... Впрочем, этого вполне достаточно. Из ста мышей нельзя составить одну кошку. Пока что эта задача не под силу ни математикам, ни механикам, ни баллистикам. Уже много лет она ждет своих Колумбов. Первооткрыватели - вперед!