Еще одна интересная возможность встречи космонавта с кораблем [1974 Авдеев Ю.Ф.

Предположим теперь, что космонавт отталкивается от корабля по направлению к центру Земли, и определим видимую с корабля траекторию его движения.

На рис. 43 изображены орбиты корабля и космонавта, точками 1′-8′ отмечены последовательные положения корабля на орбите через 1/8 периода обращения, а точками 1-8 - положения космонавта в те же моменты времени.

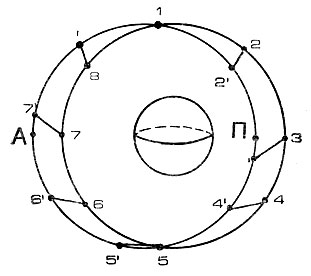
Рис. 43. Схема расположения орбит корабля и космонавта при отделении космонавта по направлению к Земле

Отталкиваясь в указанном направлении, космонавт уже сходит с первоначальной круговой орбиты, по которой двигался вместе с кораблем, а орбита его становится эллиптической. При этом периоды обращения вокруг Земли будут одинаковыми и для космонавта, и для корабля. (Строго говоря, периоды обращения будут одинаковыми только в том случае, если после отделения космонавта скорость его полета относительно Земли сохранится равной скорости корабля. Это произойдет лишь тогда, когда векторы скорости корабля и скорость отделения космонавта от корабля образуют равнобедренный треугольник. Значит, космонавт, отталкиваясь, должен на ничтожную величину отклониться от направления на центр Земли в сторону полета. Для простоты мы это отклонение не учитываем.) Следовательно, через каждый виток корабль и космонавт будут одновременно приходить в точку их разделения. Перигей и апогей орбиты космонавта на рис. 43 обозначены точками П и А соответственно. Как известно, скорость полета в перигее всегда больше скорости полета в апогее. Поэтому на первом полувитке (точки 2, 3, 4, 5) космонавт будет обгонять корабль, удаляясь от него, а на втором (точки 6, 7, 8, 1) приближаться к нему. По завершении витка описанный процесс будет повторяться.

Таким образом, при отталкивании в направлении к центру Земли космонавт будет определенным образом колебаться относительно корабля в плоскости орбиты, все время находясь впереди корабля (если смотреть по направлению полета), удаляясь и приближаясь к нему с частотой, кратной периоду обращения. Одновременно с этим на первом полувитке космонавт будет находиться ниже корабля (т. е. ближе к Земле), после завершения первой половины витка будет иметь равную высоту и на втором полувитке будет двигаться выше корабля.

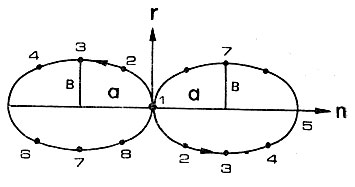
Рис. 44. Траектория движения космонавта относительно корабля при отделении космонавта в направлении к центру Земли (правая) и от центра Земли (левая). Корабль расположен в точке 1

Математический анализ показывает, что приближенно (но с высокой степенью точности!) траекторию движения космонавта относительно корабля можно представить в виде одного из эллипсов, изображенных на рис. 44. Правая траектория соответствует случаю отделении космонавта в направлении к центру Земли, а левая - от центра Земли. Такие траектории часто называют критическими. Характерной особенностью критических траекторий является то, что независимо от радиуса орбиты корабля форма их остается одной и той же, т. е. эксцентриситет имеет всегда постоянное значение, примерна равное 0,873. Любопытно также, что большая полуось критической траектории в два раза больше малой полуоси. При скорости отделения космонавта 1 м/сек наибольшее удаление его от корабля (через половину периода; точка 5 на рис. 44) составит 3,8 км вдоль орбиты и отклонение вверх и вниз - 0,95 км. При полете по орбите спутника Луны с высотой 100 км аналогичные отклонения составят 4,5 км и 1,12 км соответственно.

Таким образом, радиальное отделение космонавта от корабля в приближенном представлении приводит к относительному движению по замкнутой траектории, имеющей форму эллипса, который может лежать как впереди космического корабля (в направлении полета), так и позади. Исходя из этой особенности движения, вы теперь в состоянии ответить на следующий вопрос: как полетит относительно корабля камень, брошенный к Земле? На этот вопрос мы ответим следующим примером.

Во время полета космического корабля "Восход-2", пилотируемого летчиками-космонавтами П. И. Беляевым и А. А. Леоновым, был осуществлен впервые в мире выход человека из корабля в космическое пространство. После осуществления полета космонавт А. А. Леонов рассказал, что при нахождении в открытом космосе им была отброшена к Земле одна оказавшаяся ненужной деталь. В привычном для нас представлении выражение "деталь была отброшена к Земле" означает, что в дальнейшем она будет все более и более удаляться от корабля и в конце концов упадет на Землю подобно тому, как падает на Землю брошенный с вышки камень. Однако проведенный выше анализ показывает, что подобного, привычного для земных, не космических, жителей движения брошенной к Земле детали в действительности происходить не будет.

Предположим для простоты, что орбита корабля-спутника "Восход-2" была круговой, а космонавт А. А. Леонов отбросил деталь по радиусу орбиты ("к Земле"). В этом случае в начале своего движения брошенная деталь действительно будет удаляться от корабля по направлению к Земле, но одновременно с этим начнет обгонять его. Спустя четверть периода обращения корабля вертикальное (т. е. к Земле) перемещение детали прекратится, причем она будет находиться впереди и ниже корабля. В последующем она начнет перемещаться вверх, уменьшая свою горизонтальную составляющую скорости и через половину периода обращения выйдет на орбиту корабля впереди него. Далее деталь начнет подниматься над орбитой, смещаясь одновременно к кораблю, и после завершения витка вплотную подойдет к нему. Если только она не столкнется с кораблем, то в дальнейшем описанный характер движения будет повторяться.

Таким образом, привычное для нас представление о падении брошенного с вышки камня нельзя распространять на движение брошенной с корабля детали, так как в последующем она неограничена в своем движении. Брошенная космонавтом А. А. Леоновым деталь не упала на Землю, а в течение полета двигалась в его окрестности, периодически приближаясь и удаляясь от него.

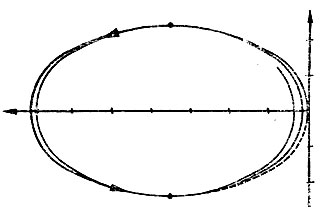
Рис. 45. Траектория относительного движения космонавта, рассчитанная точными методами (сплошная линия) и по приближенным формулам (пунктирная линия)

Необходимо еще раз оговориться, что критические траектории могут быть образованы, строго говоря, при движении в центральном гравитационном поле сил. Наличие различных возмущений (нецентральность поля, сопротивление атмосферы и др.) даже при условии абсолютно точного отделения космонавта не позволит создать строго периодические (критические) орбиты, которые бы заканчивались возвращением космонавта точно на корабль. Однако, как указывалось ранее, при небольших скоростях отделения космонавта орбиты космонавта и корабля по отношению к размерам Земли будут достаточно близкими и на их относительное движение будет влиять лишь разность возмущающих сил. Если возмущающие силы по отношению к силам притяжения планеты по своей величине составляют первый порядок малости, то упомянутая разность возмущающих сил будет являться величиной второго порядка малости. Ввиду этого в первом приближении можно считать, что относительное движение определяется лишь действием сил центрального поля и с этих позиций рассматривать периодическое движение. Это подтверждается, в частности, результатами расчетов, представленными в виде графика на рис. 45. На этом рисунке дана проекция траектории относительного движения космонавта на плоскости орбиты корабля, от которого он отделился со скоростью 10 м/сек в направлении радиуса. Сплошная линия изображает траекторию, полученную точными расчетами с учетом сжатия Земли и сопротивления атмосферы, а пунктирная - при движении в центральном поле без учета возмущений с использованием приближенных формул почти кругового движения. Приведенные результаты наглядно иллюстрируют периодический характер движения космонавта относительно корабля, несмотря на влияние возмущающих сил, а также подтверждают возможность использования для расчетов формул почти кругового движения.

Следует, наконец, отметить, что практическая реализация критических траекторий ввиду высоких требований к точности ориентации направления отделения космонавта связана со значительными техническими трудностями и поэтому едва ли может быть осуществлена на практике. Однако всегда может оказаться возможным отделение космонавта произвести в направлении, достаточно близком к радиальному и тем самым обеспечить почти периодическое движение космонавта относительно корабля. Вот только по этой причине все траектории, образованные в результате отделения космонавта почти в радиальном направлении, часто относят к периодическим.

Выявленные особенности движения открывают крайне любопытные возможности превращения космонавта в своеобразного спутника собственного корабля. Космонавт - спутник спутника. Для этого он должен вначале удалиться на некоторое расстояние от корабля в направлении его полета. После этого с помощью индивидуального реактивного двигателя космонавт разгоняется вдоль радиуса орбиты (от Земли). Величина добавки скорости определяется в зависимости от размеров эллипса, который он желает получить. В результате выполнения этих операций космонавт начнет двигаться по эллиптической траектории, внутри которой будет находиться корабль-спутник. Если до включения двигателя космонавт оказался позади корабля, то дополнительная скорость должна иметь обратное направление.

В итоге получается довольно сложная картина движения:

- траектория движения космонавта относительно корабля - эллиптическая.

При этом необходимо оговориться, что эллиптическая траектория относительного движения, за исключением формы, ничего не имеет общего с эллиптическим движением космонавта вокруг Земли, т. е. закономерности движения здесь совершенно иные. Например, эта траектория имеет всегда один и тот же эксцентриситет, скорости относительного движения в перигее и апогее всегда равны между собой, а большая ось эллипса совпадает с направлением полета корабля. Образно говоря, центр этого эллипса как бы связан с некоторой движущейся со скоростью корабля точкой орбиты, ось эллипса всегда касается орбиты, т. е. эллипс совершает "полет" по орбите корабля.