Корабль и космонавт обгоняют друг друга вопреки, казалось бы, здравому смыслу

Предположим, наконец, что космонавт отталкивается от корабля в направлении, совпадающем с вектором скорости полета. На рис. 46 показаны орбиты корабля и космонавта для этого варианта полета, - причем левый рисунок соответствует случаю отделения космонавта в направлении полета корабля, правый - "в противоположном направлении.

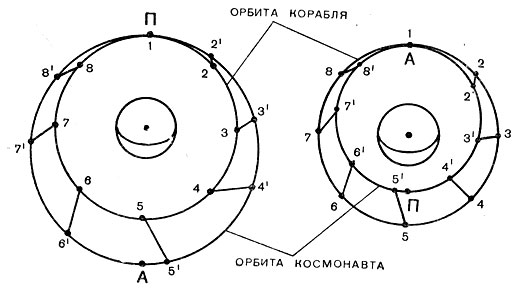
Рис. 46. Схема расположения орбит корабля и космонавта при отделении космонавта в направлении скорости полета (левый рисунок) и навстречу ей (правый рисунок)

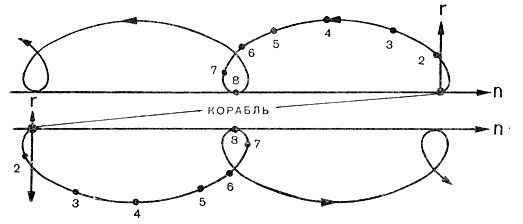
Рис. 47. Траектория движения космонавта относительно корабля при отделении в направлении скорости полета (верхний рисунок) и навстречу ей (нижний рисунок)

В первом случае вследствие увеличения скорости космонавта орбита его становится эллиптической, полностью охватывающей орбиту корабля. Период обращения космонавта станет больше периода обращения корабля, и поэтому после завершения витка космонавт отстанет от корабля. Парадоксально, но факт - увеличение скорости космонавта приводит к тому, что он отстает от корабля. Относительное положение космонавта и корабля в процессе полета на одном витке отмечено точками 2′ - 2, 3′ - 3 и т. д.

Во втором случае эллиптическая орбита космонавта будет целиком лежать внутри круговой орбиты корабля, период обращения его уменьшится. А это значит, что уменьшение скорости космонавта в конечном счете приведет к тому, что он обгонит в своем движении корабль. На рис. 47 показаны траектории движения космонавта относительно корабля для двух указанных случаев отделения. Такого вида кривые в математике носят название удлиненных циклоид (трохоид). Расстояние между петлями кривой соответствует величине отставания (или обгона) космонавта от корабля за один виток.

При скорости отделения космонавта 1 м/сек эта величина для случая движения спутника по круговой орбите с высотой 200 км составит за один виток примерно 17 км.

Обратим еще раз ваше внимание на другую сторону парадоксальности полученного результата. Предположим, что притяжение Земли и каких-либо других планет отсутствует, т. е. в этом смысле мы находимся в абсолютно пустом пространстве. Возьмем какой-либо предмет и отбросим его от себя со скоростью 1 м/сек, т. е. с той же самой скоростью, с которой космонавт оттолкнулся от корабля. После отбрасывания названный предмет будет совершать равномерное прямолинейное движение и за 1 час 30 минут (время завершения кораблем одного витка) он удалится от нас на расстояние 5,4 км. За это же время космонавт удалится от корабля на 17 км, т. е. в три раза большее расстояние. Как объяснить столь странный результат? В этом нетрудно догадаться: из-за изменения высоты полета происходит "перекачка" кинетической энергии космонавта в потенциальную и обратно и это автоматически приводит к изменению скорости полета космонавта, и, следовательно, к величине отставания или обгона корабля. Этот пример лишний раз демонстрирует особенности свободного движения космических объектов в гравитационных полях и поэтому заставляет относиться к ним с надлежащей осторожностью.

Но вернемся к рис. 47. На нем точками 2, 3... отмечены последовательные положения космонавта относительно корабля. Отсюда легко определяется видимое с корабля движение космонавта. Если, например, космонавт оттолкнулся в направлении скорости полета, то первоначально он действительно несколько обгоняет корабль, одновременно поднимаясь над горизонтом. Однако уже через 10 мин полета (спустя 41° угловой дальности полета корабля) его движение вперед прекратится и космонавт после этого одновременно с повышением высоты начнет приближаться к кораблю. На 19-й минуте (спустя 73° угловой дальности полета корабля) космонавт окажется над кораблем. В дальнейшем космонавт будет удаляться от корабля, все время находясь выше его орбиты, и только по завершении витка выйдет на первоначальную высоту (точка 8 на рис. 47).

При отделении космонавта в направлении против вектора скорости корабля он будет двигаться уже ниже корабля, обгоняя его. Отрезок между петлями кривой соответствует расстоянию, на которое удаляется космонавт от корабля за один виток. С каждым последующим витком космонавт все более и более будет удаляться от корабля.

Наступит, наконец, такой момент времени, когда суммарное отставание будет равно длине витка и космонавт... приблизится к кораблю. Однако этот случай едва ли имеет практическое значение, так как для сближения с кораблем космонавту необходимо совершить около 2400 витков вокруг Земли. Если даже предположить, что космонавт в состоянии выдержать столь длительный полет, то его может ожидать новая неприятность. Встреча его с кораблем может произойти тогда, когда петля кривой, показанная на рис. 47, будет находиться в районе местонахождения корабля. В противном случае космонавт может оказаться ниже или выше корабля на 4 км.

Таким образом, отделение в направлении полета корабля (или в противоположную сторону), если не принять специальных мер, особенно опасно для космонавта: в этом случае он практически никогда не вернется на корабль.

Рассматриваемому случаю относительного движения космонавта можно дать иную геометрическую интерпретацию. Математический анализ уравнений движения показывает, что движение космонавта относительно корабля можно формально представить как сумму движений по некоторой эллиптической траектории и смещение этой траектории вдоль орбиты корабля.

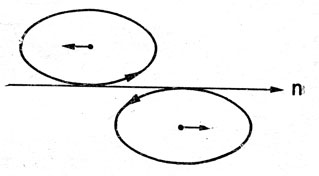
Рис. 48. Эллипсы относительного движения

Расположение этого эллипса относительно орбиты корабля показано на рис. 48. Когда космонавт оттолкнулся от корабля, он начинает полет по этой эллиптической траектории, которая смещается вдоль орбиты корабля. В результате сложения движения образуется траектория, которая была показана на рис. 47.

При отделении космонавта со скоростью 1 м/сек характеристики эллипса принимают следующие численные значения:

большая полуось - 7,6 км;

малая полуось - 3,8 км;

расстояние от орбиты до центра эллипса - 3,8 км;

скорость смещения центра эллипса вдоль орбиты - 3 м/сек.

Из приведенных данных следует, что эллипс всегда касается орбиты корабля. Если отделение космонавта происходит в направлении полета корабля, то эллипс будет расположен выше орбиты и его смещение будет происходить навстречу движению корабля. Когда космонавт отталкивается в обратную сторону, то эллипс опускается ниже орбиты и, касаясь ее, обгоняет корабль. С геометрических позиций различие в относительном движении космонавта при радиальном отделении и отделении вдоль скорости состоит в том, что в первом случае эллиптическая траектория движется вместе с кораблем и центр ее лежит на орбите корабля, а во втором случае эллипс обгоняет корабль или отстает от него, касаясь орбиты корабля сверху или снизу.

Скорость "полета" или скольжения эллипса остается всегда постоянной и равна утроенной скорости отделения космонавта. Иногда говорят, что эллиптическая траектория относительного движения дрейфует вдоль орбиты с постоянной скоростью дрейфа, словно бы ее увлекают некие космические течения. Правда, космонавт не ощутит приятного освежающего дуновения "ветерка", однако учитывать его воздействие, очевидно, необходимо.