Пешеходные тропы космонавта запутываются еще больше

Мы убедились, что траектория движения космонавта относительно корабля зависит от направления его отталкивания. Из курса механики известно, что вектор скорости движения любого тела (в нашем случае вектор скорости отделения космонавта от корабля) можно всегда разложить на три составляющие. Следовательно, в каком бы направлении ни оттолкнулся космонавт, вектор его дополнительной скорости можно представить как сумму векторов скоростей, направленных вдоль Осей транспортируемой системы координат. И чтобы найти результирующую траекторию движения при произвольном направлении отделения космонавта, достаточно определить составляющие вектора скорости вдоль осей системы координат.

Возможные варианты, характеризующие направление отделения космонавта от корабля, приведены в табл. 5. Выше были рассмотрены первые три наиболее простых варианта. Теперь выясним особенности движения космического пешехода в других случаях его отделения от корабля. Можно сразу же сказать, что эти траектории будут иметь более сложный вид.

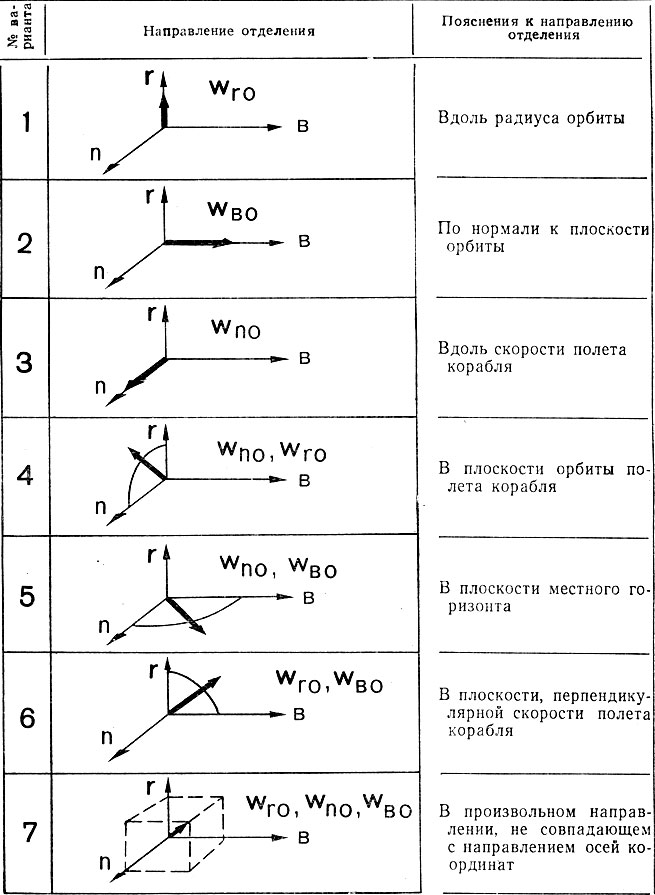
Таблица 5. Варианты направлений отделения космонавта от корабля

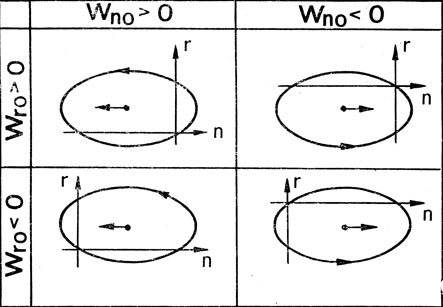
Рис. 49. Эллипсы относительного движения при отделении космонавта в плоскости орбиты корабля

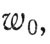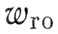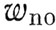Вариант 4. Космонавт отделяется в любом направлении в плоскости орбиты корабля со скоростью имеющей проекции и Понятно, что траектория его относительного движения будет лежать в плоскости орбиты. Оказывается, что в этом случае траекторию движения космонавта можно представить как сумму движений по эллипсу, смещающемуся вдоль орбиты корабля. В частности, при полете на орбите ИСЗ с высотой 200 км и отделении космонавта со скоростью, проекции которой равны 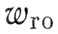= = 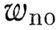1 м/сек, получим:

большая полуось - 3,9 км;

малая полуось - 1,95 км;

скорость дрейфа эллипса вдоль орбиты - 3 м/сек.

Анализ движения показывает, что в рассматриваемом случае отделения космонавта размеры эллиптической траектории относительного движения зависят от величины скорости отделения, тогда как эксцентриситет ее остается неизменным. Центр эллипса располагается либо над орбитой корабля (при 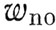> 0), либо находится ниже ее (при 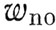< 0). В момент начала свободного полета космонавта центр эллипса располагается позади корабля, когда 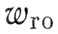> 0, и впереди его, когда 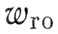< 0. Схема расположения эллиптической траектории относительно транспортируемой системы координат при различных сочетаниях знаков компонентов скорости отделения (т. е. направлении ее) в момент отделения космонавта приведена на рис. 49. В дальнейшем космонавт совершает полет по одному из указанных эллипсов, который в свою очередь дрейфует со скоростью 3. Этот рисунок объединяет все случаи движения космонавта при отделении от корабля в плоскости его орбиты.

Теперь можно сформулировать основные особенности движения космонавта относительно корабля для рассматриваемого случая отделения:

1. Траектория движения космонавта слагается из полета по эллипсу и перемещения эллипса вдоль орбиты корабля с постоянной скоростью; в частности, при радиальном отделении, эллипс остается неподвижным.

2. Облет эллипса происходит всегда в одном и том же направлении, противоположном вращению спутника вокруг Земли, и время одного оборота равно периоду обращения спутника.

3. Большая ось эллипса остается всегда параллельной текущему направлению вектора скорости корабля.

4. Размеры эллипса зависят от величины скорости отделения космонавта, но эксцентриситет его имеет во всех случаях одно и то же значение.

5. Центр эллипса может располагаться над орбитой, на самой орбите и под нею; крайние положения эллипса - касание орбиты корабля сверху или снизу.

Необходимо отметить еще одно обстоятельство: если в произвольный момент времени полета космонавт с помощью индивидуального реактивного двигателя изменит горизонтальную составляющую скорости полета относительно корабля на величину 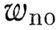, то дрейф эллипса прекратится и космонавт начнет облет корабля по неизменной эллиптической траектории. Таким образом, чтобы космонавт стал спутником корабля, он должен выполнить следующие операции:

- отделиться от корабля в произвольном направлении в плоскости орбиты его движения, запомнив при этом величину проекции скорости отделения на направление полета корабля;

- в произвольный момент времени с помощью реактивного двигателя изменить свою скорость полета на величину , но противоположную ей.

После выполнения этих операций "пешеходная тропа" космонавта замкнется вокруг корабля и он 'будет вечно "прогуливаться" по ней, не затрачивая для этого никаких усилий.

Вариант 5. Космонавт отталкивается от корабля в направлении, параллельном горизонту Земли, со скоростью 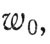, имеющей проекции ,

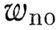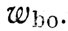
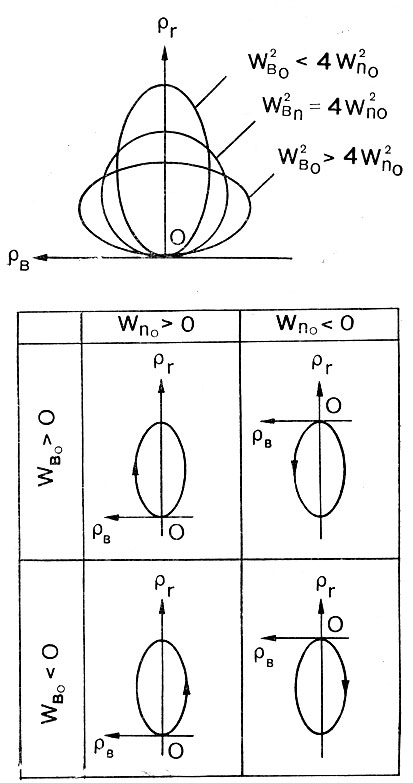
Рис. 50. Проекции траекторий относительного движения космонавта на плоскость, перпендикулярную вектору скорости, при отделении космонавта в плоскости местного горизонта

Как уже было показано ранее, за счет составляющей скорости , направленной вдоль скорости полета корабля, будет наблюдаться систематический уход космонавта от корабля и на величину этого ухода нормальная составляющая скорости не будет оказывать какого-либо влияния, поскольку за счет ее наблюдается только отклонение космонавта в сторону от орбиты. Значит, в этом случае отделения проекция траектории движения космонавта на плоскости орбиты останется точно такой же, какой она получается при отделении вдоль скорости. Но составляющая скорости 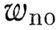одновременно вызывает перемещение космонавта вверх или вниз от орбиты корабля. Значит, если провести плоскость, перпендикулярную вектору скорости корабля, то проекция траектории космонавта на эту плоскость при скорости отделения космонавта с компонентами 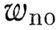, 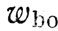опишет некоторую кривую. Общий вид этих кривых показан на рис. 50. Оказывается, что они могут представлять собой эллипсы, различным образом ориентированные относительно осей координат. Размеры эллипсов, их ориентация и эксцентриситет зависят от соотношения скоросте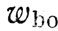й и 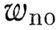. Когда , то ось эллипса параллельна оси Ob транспортируемой системы координат, т. е. направлена по нормали к плоскости орбиты. С увеличением 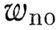эллипс "округляется" и при выполнении условия 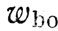= 2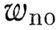, превращается в окружность. Наконец, если 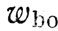<2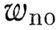, то ось эллипса совпадает с радиусом орбиты. Положение этих эллипсов относительно корабля при различных направлениях отделения космонавта в плоскости местного горизонта показаны на рис. 50.

Таким образом, в описываемом варианте отделения космонавта траектория его последующего движения будет целиком умещаться внутри цилиндра, ось которого направлена вдоль орбиты полета корабля. В процессе полета космонавт как бы скользит по стенкам цилиндра, описывая удаляющуюся от корабля спираль.

Вариант 6. Космонавт отделяется от корабля импульсом 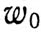компонентами 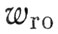, , 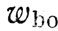т. е. в плоскости, перпендикулярной вектору скорости полета корабля. В этом случае траектории относительного движения космонавта в проекции на эту плоскость будут также замкнутыми кривыми, имеющими форму эллипсов либо окружности. При этом не следует путать форму траектории с ее проекцией, поскольку последняя, если смотреть с корабля, выглядит достаточно просто.

Движение космонавта будет происходить внутри цилиндра, имеющего в сечении одну из фигур, изображенных на рис. 51, при ограниченной длине его. Длина цилиндра будет равна наибольшему расстоянию, на которое удаляется космонавт при радиальном отделении от корабля. Однако сколько бы ни продолжался полет, космонавт внутри цилиндра будет описывать одну и ту же траекторию, повторяющуюся от витка к витку.

Вариант 7. Это наиболее общий случай отделения космонавта, когда ни одна из компонент скорости отделения не равна нулю. Вся траектория относительного движения космонавта будет также расположена внутри цилиндра, имеющего в сечении форму эллипса и касающегося орбиты корабля. Внутри этого цилиндра космонавт будет описывать сложную спиралевидную кривую, удаляющуюся от корабля и касающуюся "стенок" цилиндра.

Таковы общие характеристики траектории движения космонавта относительно корабля. Существенно отметить, что для того, чтобы космонавт мог вернуться на корабль после прогулки в космосе, он должен оттолкнуться от корабля в любом направлении, перпендикулярном вектору скорости его полета. Описав замкнутую кривую, космонавт самопроизвольно вернется на корабль. Возвращение при этом произойдет либо через половину витка, либо через виток.

В реальных условиях космонавт никогда не сможет оттолкнуться от корабля строго перпендикулярно вектору скорости его полета. При произвольном отталкивании вектор дополнительной скорости космонавта всегда будет иметь составляющую, которая совпадет с вектором скорости корабля. Достаточно помнить, что столь мизерная составляющая скорости, как 1 см/сек, спустя виток уведет космонавта от корабля почти на 0,2 км. Поэтому в реальном случае космонавт не может рассчитывать на идеальное направление своего отталкивания, при котором его возвращение на корабль происходит само собой.

Вот почему трос, соединяющий космонавта с кораблем, который использовался при всех выходах человека в космос, есть не просто элемент страховки, как, скажем, страховочный трос циркового акробата. Трос, соединяющий "безмоторного" пешехода в космосе с кораблем, - это совершенно необходимый -атрибут космической прогулки, без которого сама эта прогулка вообще немыслима.

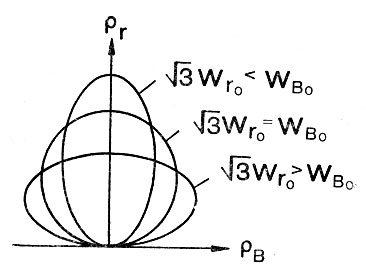
Рис. 51. Проекции траектории относительного движения космонавта на плоскость, перпендикулярную вектору скорости корабля, при отделении его импульсом, лежащим в этой плоскости