Движение планет

Удивительно замысловаты видимые пути планет среди звезд. Двигаясь в одну сторону, они иногда неожиданно останавливаются и начинают пятиться назад. А потом вскоре попятное движение прекращается, и планета вновь идет в прежнем, прямом направлении. Надо добавить, что видимые движения планет неравномерны. Все это вызывало недоумение древних и в свое время породило громоздкую ситему Птолемея, преобразованную в XVI в. Коперником.

Однако и Копернику не удалось объяснить некоторые неравномерности в движении планет, не говоря уже о других более тонких деталях. Только "законодатель неба" немецкий астроном Иоганн Кеплер (1571-1630) сумел внести полную ясность в законы движения планет, а Ньютон нашел теоретическое объяснение этим законам. Чтобы выяснить, как это произошло, введем некоторые понятия, широко употребляемые в современной астрономии.

Относительно Солнца и Земли планеты при их движении по орбитам могут занимать различные положения, или, как их называют астрономы, конфигурации (рис. 31). Планеты, например, могут оказаться в одной, перпендикулярной эклиптике плоскости, проходящей через центры Земли (3) и Солнца (С). Если при этом Солнце расположено между внутренней планетой и Землей, такая конфигурация планеты называется верхним соединением с Солнцем (положение 6). Меркурий и Венера могут иногда оказаться между Землей и Солнцем (положение 8). Такое их расположение называется нижним соединением^*. Очевидно, в момент нижних соединений с Солнцем иногда можно наблюдать прохождение планеты по солнечному диску.

^* (Так как внешне планеты, расположенные от Солнца дальше, чем Земля, в нижнем соединении быть не могут, говорят просто о соединении внешних планет с Солнцем. )

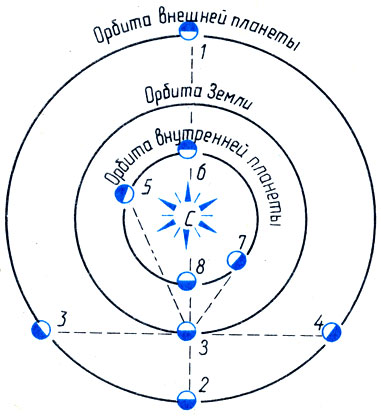
Рис. 31. Конфигурации планет

Планеты более далекие от Солнца, чем Земля, по временам могут находиться в области неба, противоположной Солнцу. В эти моменты Земля находится между планетой и Солнцем. Такая конфигурация планеты называется ее противостоянием: данная планета на небе как бы "противостоит" Солнцу (положение 2). При противостояниях планеты видны всю ночь и расстояния до них являются наименьшими.

Угол между лучами, идущими с Земли к Солнцу и планете, называется элонгацией планеты, причем различают западные (к западу от Солнца) и восточные элонгации (положения 5 и 7). В момент соединения элонгация планеты равна нулю, в момент противостояния 180°. Наибольшая элонгация Венеры близка к 48°, а Меркурия к 29°. Элонгации, равные 90°, называются квадратурами (положения 3 и 4).

Изучая расположение планет в пространстве для различных моментов времени, можно установить, по каким законам планеты обращаются вокруг Солнца и каковы их взаимные относительные расстояния. Представьте себе (рис. 32), что Марс (М) находится в противостоянии. Затем через несколько месяцев Земля перешла в точку З₁, а Марс в точку М₁ (он движется медленнее Земли). В треугольнике 3₁М₁С угол СЗ₁М₁ есть элонгация Марса, определяемая из наблюдений. Угол М₁СЗ₁ находим как разность угловых смещений Земли и Марса от момента противостояния. Значит, в рассматриваемом треугольнике известны все углы, а тогда по теореме синусов

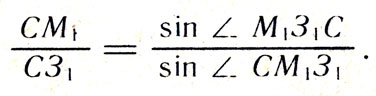
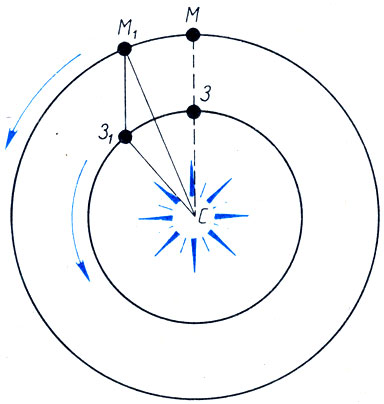
Рис. 32. Относительные расстояния планет

Так можно определить, во сколько раз Марс дальше от Солнца, чем Земля. Таким же образом находят относительные расстояния до всех других тел Солнечной системы, т. е. удаленность от Земли в астрономических единицах. Чтобы выразить эти расстояния в километрах, надо возможно точнее измерить "астрономическую единицу"- расстояние от Земли до Солнца. Во времена Кеплера были известны лишь относительные расстояния планет. Они-то и фигурируют в его законах.

Первые два закона движения планет, сформулированные Кеплером, были опубликованы в 1609 г. в его книге "Новая астрономия", а третий, открытие которого стоило ему наибольшего труда,- в 1619 г. в книге "Гармония мира".

В своих сочинениях Кеплер не раз высказывал мысль, что сила, управляющая движением планет, исходит от Солнца. Но найти закон действия этой силы ему не удалось.

"Законодатель неба" умер на 59-м году жизни в обстановке разрухи, вызванной Тридцатилетней войной. Оставшееся от Кеплера имущество состояло из нескольких десятков книг и... семи пфеннигов! Но законы, им открытые, обессмертили его имя. Вот эти законы.

Первый закон. Орбиты планет суть эллипсы, в одном из фокусов которых находится Солнце.

Эллипсом, как известно, называется плоская замкнутая кривая, сумма расстояний от любой точки которой до двух данных точек, называемых фокусами эллипса, есть величина постоянная. Наибольшая хорда эллипса, на которой лежат оба фокуса, называется осью эллипса, а ее половина - большой полуосью. Чем дальше отстоят друг от друга фокусы эллипса (при постоянной большой оси), тем более он вытянут; чем ближе фокусы друг к другу, тем меньше эллипсы отличаются от окружности; при совпадении обоих фокусов в одной точке эллипс превращается в окружность. Заметим, что орбиты всех крупных планет близки к окружностям.

Из первого закона Кеплера следует, что расстояние каждой планеты от Солнца непрерывно изменяется в некоторых пределах - от наибольшего к наименьшему, и обратно.

Ближайшая к Солнцу точка орбиты планеты называется перигелием, а наиболее далекая - афелием.

Второй закон (закон площадей). Радиус-вектор планеты описывает в равные" времена равновеликие площади.

Радиусом-вектором планеты называют отрезок прямой, соединяющей планету с Солнцем (рис. 33). Допустим, что заштрихованные площади описаны радиусом-вектором планеты за одинаковое время. Из рисунка 33 видно, что равенство этих площадей может быть только в том случае, если дуги, пройденные планетой, неодинаковы. Отсюда следует, что планеты движутся по своим орбитам неравномерно - чем ближе к Солнцу, тем быстрее, чем дальше от Солнца, тем медленнее.

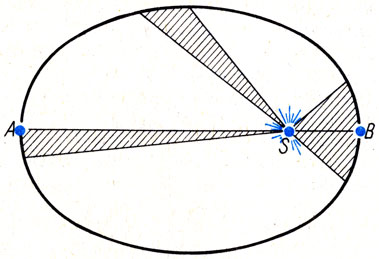
Рис. 33. Второй закон Кеплера

Второй закон Кеплера иначе называется законом площадей.

Третий закон. Квадраты времен обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.

Большие полуоси орбит планет равны их среднему расстоянию от Солнца, и потому в формулировке закона слова "больших полуосей их орбит" можно заменить словами "их средних расстояний от Солнца". Пусть Т₁ и Т₂ - периоды обращения планет вокруг Солнца, а а₁ и а₂ - их средние расстояния от Солнца. Тогда третий закон Кеплера может быть выражен формулой:

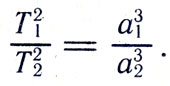
Законы Кеплера выражают свойства движения планет, полученные из наблюдений. Но почему планеты движутся именно так, объяснить удалось лишь Исааку Ньютону.