Ньютон и Кеплер

Ньютон сформулировал следующую "задачу двух тел": даны две материальные точки с массами m₁ и m₂, начальными скоростями v₁ и v₂ и известным начальным положением в некоторой системе координат. Найти, как будут двигаться обе точки, если между ними действует сила взаимного тяготения.

Уточним, что под материальными точками Ньютон понимал такие тела, размерами которых в данном конкретном случае можно пренебречь по сравнению с расстояниями между ними. Так, например, изучая движение планет в Солнечной системе, можно считать их материальными точками - слишком малы сами планеты в сравнении с расстояниями друг от друга и до Солнца. Но та же планета Земля и географами и геофизиками, конечно, не считается материальной точкой. Для них это огромное тело со сложной структурой. Кстати, если небесное тело обладает сферическим распределением плотности, т. е. внутри тела плотность зависит только от расстояния до центра (слоистое тело), то в таком случае тела притягивают друг друга как материальные точки, т. е. так, как если бы вся их масса была сосредоточена в их центре.

Средствами высшей математики Ньютон получил следующее решение.

Если одно из тел считать неподвижным (что всегда возможно), то орбитой второго тела относительно первого будет лишь одна из трех кривых - эллипс, гипербола или парабола. Все эти кривые легко получить, рассекая коническую поверхность плоскостью, поэтому они называются коническими сечениями. Других орбит в задаче двух тел не существует.

Ньютон сделал и нечто большее. Он доказал, что все три закона Кеплера есть следствие закона всемирного тяготения и основных Законов механики. Иначе планеты к двигаться не могут. Другая картина движения возникла бы лишь в том случае, если бы изменился закон силы, т. е., скажем, сила стала бы действовать обратно пропорционально кубу расстояния. В рамках же закона Ньютона "кеплеровское" движение в задаче двух тел неизбежно.

Проводя строгие математические расчеты, Ньютон уточнил третий закон Кеплера. Оказалось, что более точно он выглядит так:

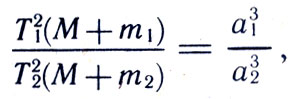
где М - масса Солнца, а m₁ и m₂ - массы планет. Так как массы планет ничтожно малы по сравнению с массой Солнца, дробь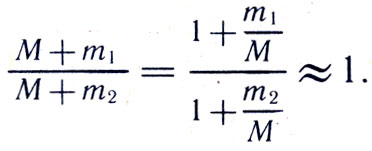Полагая эту дробь равной 1, получаем третий закон Кеплера в его первоначальной форме.

Можно решить и обратную задачу - из законов Кеплера вывести закон всемирного тяготения. Этот факт еще раз доказывает, как тесно связаны между собой все четыре закона.

Несмотря на почести, оказанные Исааку Ньютону, некоторые из его современников скептически отнеслись к его открытиям. Известный физик и астроном Гюйгенс высмеивал идеи Ньютона о всемирном тяготении. Великий философ и математик Лейбниц поначалу считал выкладки Ньютона сомнительными. А Иоганн Бернулли в 1730 г. получил премию Парижской Академии наук за сочинение, в котором пытался объяснить форму планетных орбит, не прибегая к закону тяготения.

Как и все новое, ньютониан-ская физика лишь постепенно получала признание. Требовались факты, которые могли бы наглядно и убедительно доказать способность закона тяготения объяснять и предсказывать космические явления.