Как взвесить Солнце?

В повседневной жизни тяготение тел друг к другу (кроме силы тяжести) неощутимо. Слишком ничтожно мала гравитация (т. е. тяготение) по сравнению с другими силами. Лишь исполинские массы Земли и других космических тел создают иллюзию мощности тяготения. Но только очень тонкими экспериментами удается измерить, как притягивают друг друга небольшие тела.

Первый успешный опыт такого рода был проделан еще в 1798 г. соотечественником Ньютона Г. Кавендишем (1731-1810). Его установка, получившая название крутильных весов (рис. 34), состояла из двух маленьких шариков (в), соединенных стержнем, который подвешивался на кварцевой нити. Вблизи этих шариков Кавендиш помещал два массивных свинцовых шара (В). Эти шары, притягивая концы стержня, закручивали кварцевую нить. По закручиванию нити можно вычислить силу притяжения F. По закону тяготения

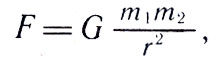
где m₁ и m₂ - массы маленьких шариков, r - расстояние между ними и большими шарами, a G - коэффициент пропорциональности, называемый постоянной тяготения, значение которого можно определить из указанной формулы:

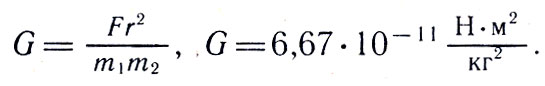
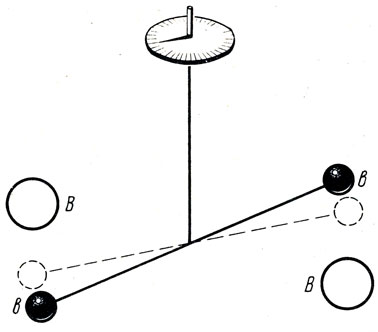
Рис. 34. Крутильные весы Кавендиша

Зная G и используя закон тяготения, можно определить массу Земли и других космических тел. В самом деле, пусть масса Земли М. Тогда любое тело массой т притягивается Землей с силой

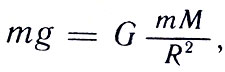
где R - радиус Земли. Отсюда масса земного шара равна

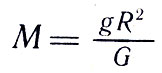
Подставив в формулу известное значение величин, получим

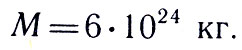
По закону тяготения Земля и Луна обращаются вокруг общего центра тяжести С, который лежит внутри Земли. Обозначим его расстояние до центра Земли буквой х. Тогда по законам механики

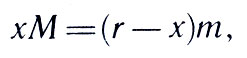
где М - масса Земли, m - масса Луны, а r - расстояние между ними. Из-за движения Земли вокруг точки С меняется астрономическая долгота Солнца (по сравнению с той, которая была бы при отсутствии такого движения). Точные астрономические измерения приводят к выводу, что х = 4635 км и, следовательно,

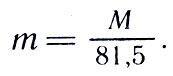
"Взвесив" Луну, или, точнее говоря, определив ее массу, можно перейти к "взвешиванию" Солнца. Пусть некоторая планета массой т имеет спутник массой m₁. Массу Солнца обозначим М, а периоды обращения планеты вокруг Солнца и спутника вокруг планеты соответственно Т и T₁. Тогда по уточненному третьему закону Кеплера следует:

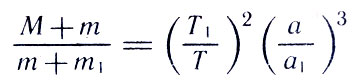
где а и a₁ - полуоси орбит планеты и спутника. Так как масса планеты мала по сравнению с массой Солнца, а у спутника много меньше, чем у планеты, приходим к приближенному равенству

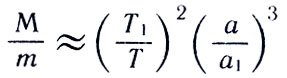
Используя в качестве планеты и ее спутника Землю и Луну, получаем, что масса Солнца примерно в 333 000 раз больше массы Земли, т. е. масса Солнца приблизительно равна 2*10³⁰ кг.

Описанные методы "взвешивания" небесных тел не всегда применимы и далеко не единственны. Но любые иные методы в конечном счете основываются на законе всемирного тяготения: неизвестную массу тела находят по гравитационному воздействию этого тела на другие тела.