Теория возмущений

Всемирное тяготение должно было в принципе объяснить движение всех небесных тел. Но тут возникли неожиданные трудности. Если в задачу двух тел, успешно решенную Ньютоном, добавить третье тело, тоже материальную точку, то ситуация усложняется необычайно. Получается задача трех тел.

Даны начальные положения, массы и скорости трех материальных точек. Предполагая, что между ними действует взаимное тяготение, найти траектории всех трех материальных точек.

Крупнейшие математики и механики XVIII и XIX вв. безуспешно пытались решить эту задачу. Лишь в 1912 г. финский математик К. Зун-дман нашел ее общее решение, но в таком виде, который исключал практическое применение. Формулы Зундмана представляют собой ряды, т.е. выражения из бесчисленного множества суммируемых членов. В таких выражениях результат получается тем точнее, чем больше просуммировать членов ряда, начиная с его первого члена. Простейший пример числового ряда - сумма членов бесконечно убывающей геометрической прогрессии. Есть ряды, составленные не из чисел, а из функций. Ряды, составленные Зундманом, принадлежат к функциональным рядам.

Однако, чтобы по ним подсчитать положение космического тела o с точностью до 10%, надо взять не меньше 10^8000000 членов ряда Зундмана. Суммирование такого колоссального числа слагаемых не под силу даже современным ЭВМ.

Правда, в некоторых частных случаях задача трех тел допускает сравнительно простое решение. Эти случаи нашел знаменитый французский математик Жозеф Лагранж (1736-1813).

Представим себе, что одно тело обращается вокруг другого по окружности. Как доказал Лагранж, существуют такие положения третьего тела, при которых взаимное расположение всех трех тел в процессе движения остается неизменным.

Пусть первым телом - будет Солнце, вторым - планета, обращающаяся вокруг Солнца по круговой орбите. Точки, в которых третье тело сохранит взаимное расположение по отношению к двум другим телам, называются либрационными точками. Первые три из них, так называемые коллинеарные либрационные тонки, L₁, L₂, L₃, расположены на прямой, проходящей через Солнце и планету (рис. 35). Их расположение на этой прямой, разумеется, зависит от масс первых двух тел и расстояния между ними. Если поместить в любую из этих точек третье тело, вся система из трех тел будет вращаться как единое тело (совсем так, как если бы вы стали вращать рисунок вокруг точки). Исследования, однако, показывают, что положение третьего тела в коллинеарных либрационных точках неустойчиво. Если это тело даже чуть-чуть, на очень малое расстояние отойдет от коллинеарных либрационных точек, назад оно уже не возвратится, а навсегда покинет эту область пространства. Не удивительно поэтому, что такой "случай Лагранжа" в природе не осуществляется.

Значительно больший практический интерес представляют треугольные либрационные точки L₄ и L₅. Они образуют с Солнцем и планетой вершины двух равносторонних треугольников (см. рис. 35), поворачивающихся во время движения как единое целое. Замечательно, что движение вблизи этих точек устойчиво. Иначе говоря, выведенное из треугольных либрационных точек третье тело при определенных начальных условиях (например, не чрезмерно большой скорости) может снова вернуться в исходное положение.

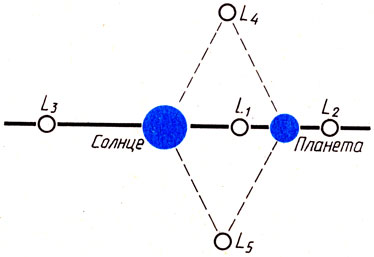
Рис. 35. Точки либрации

Еще в 1907 г. был открыт астероид Ахилл, совершающий обращение вокруг Солнца почти по орбите Юпитера. Точнее, он постоянно находится вблизи точки L₄ в системе Солнце - Юпитер. Позже открыли и другие малые планеты, демонстрирующие воплощение в природе одного из "случаев Лагранжа". Всем им присваивали имена героев Троянской войны, и потому в астрономической литературе эти замечательные астероиды называют троянцами.

В либрационных точках системы Земля - Луна в 1959 г. польский астроном С. Кордылевский обнаружил скопления пыли, получившие o название "облаков Кордылевского". Кроме случаев Лагранжа есть и другие частные случаи задачи трех тел, которые имеют решение, например, когда масса одного из тел очень мала. Но в общем виде задача трех тел, повторяем, не решена.

Представьте себе, что одно из трех тел Солнце, второе Земля, а третье, скажем, планета Марс. Если бы не было Марса, Земля обращалась бы вокруг Солнца строго по законам Кеплера. Притяжение со стороны Марса искажает, или, как говорят астрономы, возмущает движение Земли, и оно перестает быть кеплеровским.

Можно подумать, что возмущающая сила, порожденная Марсом, направлена от Земли к Марсу, но это не так. Можно доказать, что из-за сложной игры сил тяготения всех трех тел возмущающая сила все время изменяется и по числовому значению, и по направлению. По этой причине вычисление возмущений- очень сложная задача, решаемая с помощью рядов. Начало теории возмущения было положено трудами великих математиков XVIII в. Даламбером, Эйлером, Лагранжем, Лапласом, которые, собственно, и создали классическую небесную механику.

Фундаментальный пятитомный труд Пьера Лапласа "Небесная механика", написанный в бурные годы Великой французской революции, подытоживал успехи теории возмущений XVIII в. В XIX в. ее разработку продолжили Ньюкомб, Хилл, Гюльден, Пуанкаре и многие другие. В текущем веке всемирную известность приобрели небесно-механические исследования проф. Б. В. Нумерова и в особенности московского астронома, проф. Г. И. Дубошина и его школы.

Теория возмущений позволяет с очень высокой точностью рассчитывать движения космических тел - как естественных, так и искусственных. Вместе с тем она способна ответить и на такие теоретические вопросы, как проблема устойчивости Солнечной системы.

Орбита любого космического тела задается шестью величинами, или, как их называют, элементами. Три из них определяют положение орбиты в пространстве, два - размеры орбиты и ее форму и, наконец, шестой элемент - положение космического тела на орбите. Из-за возмущений все элементы меняются. Но эти изменения различны. Одни из них называются периодическими возмущениями. Как показывает их название, периодические возмущения повторяются, не выходя за некоторые ограниченные пределы. Иначе ведут себя вековые возмущения. Хотя и очень медленно, но они растут пропорционально времени. Возникает естественный вопрос - не могут ли вековые возмущения настолько изменить планетные орбиты, что Солнечная система утратит устойчивость и распадется? Проведенные исследования показали, что вековым возмущениям подвержены лишь те элементы, от которых зависит поворот орбиты в пространстве, с сохранением ее формы и наклонения к плоскости эклиптики. Судя по всему, по крайней мере на ближайшие миллионы лет устойчивость Солнечной системы обеспечена.

В XVIII и XIX вв. теория возмущений весьма помогла мореплаванию. Дело в том, что Луна обладает очень сложным движением. Его возмущают не только Солнце, но и отклонение Земли от шарообразной формы, и другие еще более тонкие эффекты. Теорией лунного движения занимались все великие небесные механики, а Леонард Эйлер посвятил этому вопросу даже специальный трактат "Теория движения Луны" (1753).

Луна обращается вокруг Земли за 27¹/₃ сут, смещаясь ежесуточно на фоне звезд примерно на 13°. Значит, наблюдая, где видна Луна на фоне звездного неба, можно узнать момент времени. Для этой цели и составлялись возможно более точные таблицы положения 1 Луны по гринвичскому времени. Мореплаватель, определив местное время описанным ранее способом, наблюдает положение Луны среди звезд и по таблицам определяет в тот же момент гринвичское время. Отсюда легко вычислить долготу местонахождения корабля, а определение его широты, как известно, не представляет особых затруднений.

Теория возмущений сыграла громадную роль и в открытии новых планет, в расширении наших представлений о Солнечной системе. Исторический пример проиллюстрирует это утверждение.